奔驰定理证明探究

1. 问题分析

奔驰定理: $O$是$\triangle ABC$内一点, 且$x\cdot\overrightarrow{OA}+y\cdot\overrightarrow{OB}+z\cdot\overrightarrow{OC}=\overrightarrow{0}$,
则$S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=x:y:z$.

从这个形式很容易联想到三角形重心的性质,
即三角形重心满足$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$, $S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=1:1:1$, 应该可以通过重心的性质证明.

2. 尝试证明

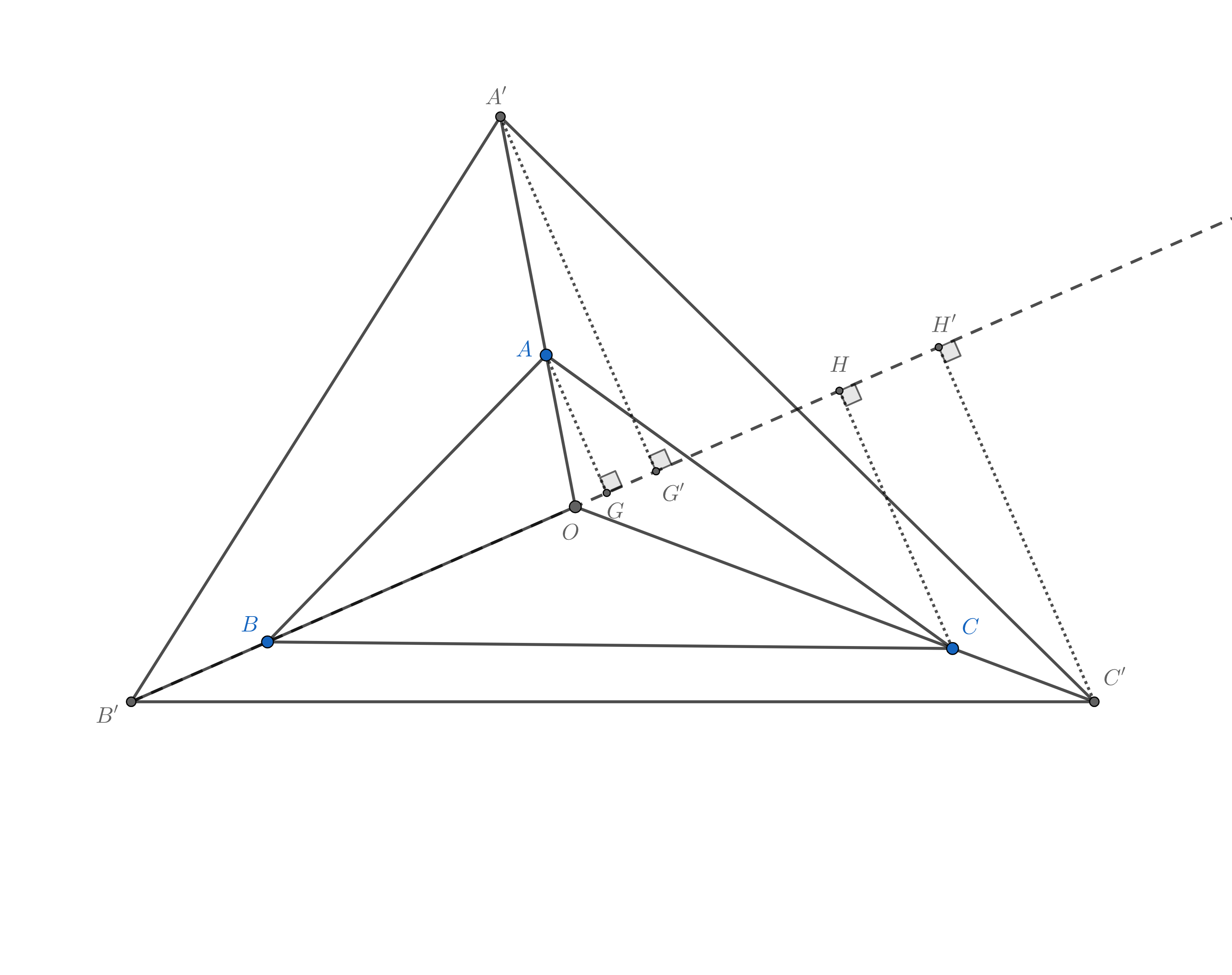
如图, $O$是$\triangle A’B’C’$的重心, $A,B,C$分别为$OA’,OB’,OC’$上一点, 由于$\triangle A’B’C’$是任意的, $\triangle ABC$也为任意三角形. 由$\overrightarrow{OA’}+\overrightarrow{OB’}+\overrightarrow{OC’}=\overrightarrow{0}$可得$\overrightarrow{OA’}=x\cdot\overrightarrow{OA}$, $\overrightarrow{OB’}=y\cdot\overrightarrow{OB}$, $\overrightarrow{OC’}=z\cdot\overrightarrow{OC}$.
过$A$作$AG\perp BO$, $A’$作$A’G’\perp BO$, $C$作$CH\perp OB$, $C’$作$C’H’\perp OB$.
由相似得$AG=\frac{1}{x}A’G’,CH=\frac{1}{z}C’H’$, 又因为$A’G’=C’H’$, 所以$CH:AG=x:z$, 可得$S_{\triangle BOC}:S_{\triangle AOB}=x:z$, 同理可证$S_{\triangle BOC}:S_{\triangle AOC}=x:y$, 即$S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=x:y:z$.
以上是一些初步思考，并不是很严格的证明。

3. 正式证明

延长$OA,OB,OC$, 使$\overrightarrow{OA’}=x\cdot\overrightarrow{OA}$, $\overrightarrow{OB’}=y\cdot\overrightarrow{OB}$, $\overrightarrow{OC’}=z\cdot\overrightarrow{OC}$.
由$O$是$\triangle A’B’C’$的重心, 可得:
$$x\cdot\overrightarrow{OA}+y\cdot\overrightarrow{OB}+z\cdot\overrightarrow{OC}=\overrightarrow{0}$$
$$S_{\triangle A’OB’}=xy\cdot S_{\triangle AOB}=S_{\triangle B’OC’}=yz\cdot S_{\triangle BOC}=S_{\triangle A’OC’}=xz\cdot S_{\triangle AOC}$$
整理得$S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=x:y:z\quad\square$

4. 另一种证明(面积比例推导)

仔细考虑即会发现上面的证明也不是很严格，充要性略有问题。于是我在网上找到了另一种证明方法。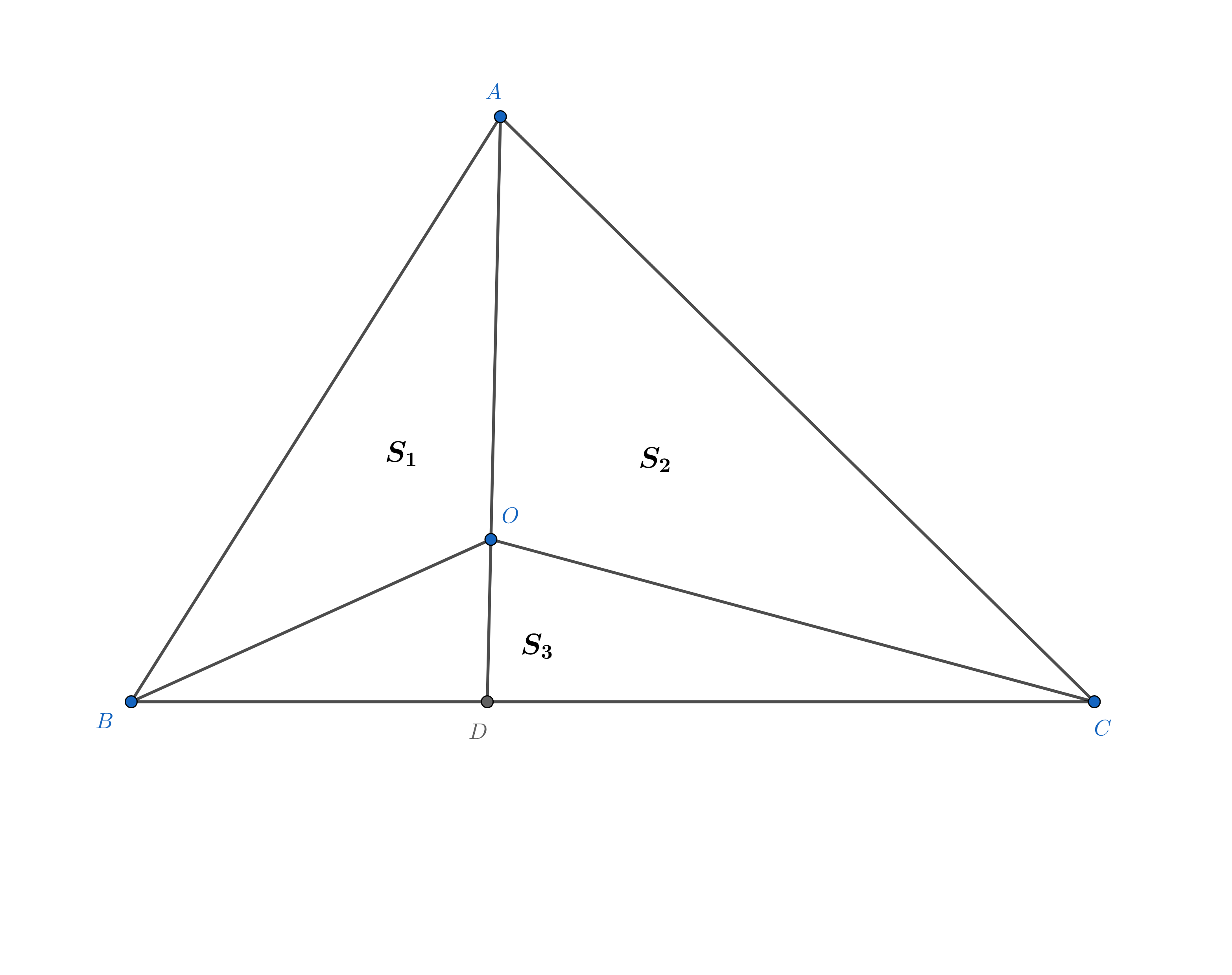

$O$为$\triangle ABC$内任意一点, 延长$AO$至$D$, 设$S_{\triangle AOB}=S_1$, $S_{\triangle AOC}=S_2$, $S_{\triangle BOC}=S_3$. 易得:
$$\overrightarrow{AO}=\frac{AO}{AD}\cdot\overrightarrow{AD}=\frac{S_1+S_2}{S_1+S_2+S_3}\cdot\overrightarrow{AD}$$
$$\overrightarrow{AD}=\frac{CD}{BC}\cdot\overrightarrow{AB}+\frac{BD}{BC}\cdot\overrightarrow{AC}=\frac{S_2}{S_1+S_2}\cdot\overrightarrow{AB}+\frac{S_1}{S_1+S_2}\overrightarrow{AC}$$
联立可得:
$$
\begin{aligned}
\overrightarrow{AO}&=\frac{S_2}{S_1+S_2+S_3}\cdot\overrightarrow{AB}+\frac{S_1}{S_1+S_2+S_3}\overrightarrow{AC}\\
&=\frac{S_2}{S_1+S_2+S_3}\cdot(\overrightarrow{AO}+\overrightarrow{OB})+\frac{S_1}{S_1+S_2+S_3}(\overrightarrow{AO}+\overrightarrow{OC})
\end{aligned}
$$
整理得:
$$\frac{S_3}{S_1+S_2+S_3}\cdot\overrightarrow{OA}+\frac{S_2}{S_1+S_2+S_3}\cdot\overrightarrow{OB}+\frac{S_1}{S_1+S_2+S_3}\cdot\overrightarrow{OC}=\overrightarrow{0}$$
即$S_3:S_2:S_1=x:y:z$, $S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=x:y:z\quad\square$

5. 特例

$\triangle ABC$三角$A,B,C$对边分别为$a,b,c$

重心

$$S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=1:1:1$$
$$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$$

内心

$$S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=a:b:c$$
$$a\cdot\overrightarrow{OA}+b\cdot\overrightarrow{OB}+c\cdot\overrightarrow{OC}=\overrightarrow{0}$$

外心

$$
\begin{aligned}
S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}&=\sin\angle BOC:\sin\angle AOC:\sin\angle AOB\\
&=\sin2A:\sin2B:\sin2C
\end{aligned}
$$
$$\sin2A\cdot\overrightarrow{OA}+\sin2B\cdot\overrightarrow{OB}+\sin2C\cdot\overrightarrow{OC}=\overrightarrow{0}$$

垂心

$$S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=\tan A:\tan B:\tan C$$
$$\tan2A\cdot\overrightarrow{OA}+\tan2B\cdot\overrightarrow{OB}+\tan2C\cdot\overrightarrow{OC}=\overrightarrow{0}$$

6. 一些推广

二维

$O$为$\triangle ABC$所在平面内任意一点, 且$x\cdot\overrightarrow{OA}+y\cdot\overrightarrow{OB}+z\cdot\overrightarrow{OC}=\overrightarrow{0}$, 则:
$$S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=\vert x\vert:\vert y\vert:\vert z\vert$$
$$S_{\triangle BOC}=\frac{\vert x\vert}{\vert x+y+z\vert}$$

一维

$O$为线段$AB$所在直线上一点, 且$x\cdot\overrightarrow{OA}+y\cdot\overrightarrow{OB}=\overrightarrow{0}$, 则:
$$L_{OB}:L_{OA}=\vert x\vert:\vert y\vert$$
$$L_{OB}=\frac{\vert x\vert}{\vert x+y\vert}$$

三维

$O$为三棱锥$A-BCD$内一点, 且$x\cdot\overrightarrow{OA}+y\cdot\overrightarrow{OB}+z\cdot\overrightarrow{OC}+k\cdot\overrightarrow{OD}=\overrightarrow{0}$, 则:
$$V_{O-BCD}:V_{O-ACD}:V_{O-ABD}:V_{O-ABC}=\vert x\vert:\vert y\vert:\vert z\vert:\vert k\vert$$
$$V_{O-BCD}=\frac{\vert x\vert}{\vert x+y+z+k\vert}$$
当$O$是三棱锥$A-BCD$内切球球心时:
$$S_{\triangle BCD}\cdot\overrightarrow{OA}+S_{\triangle ACD}\cdot\overrightarrow{OB}+S_{\triangle ABD}\cdot\overrightarrow{OC}+S_{\triangle ABC}\cdot\overrightarrow{OD}=\overrightarrow{0}$$
还没学立体几何，不会证明…

7. 参考

谷留明. 奔驰定理的应用与推广[J]. 中学数学研究,2019(09):20-21.