簡諧運動與單擺周期

1. 簡諧運動

第一種推導方法

設彈簧勁度系數為$k$，簡諧運動位移方程為：
$$x=A\sin(\omega t+\varphi)$$
直接求導得速度：
$$v=\frac{\mathrm{d}x}{\mathrm{d}t}=A\omega\cos(\omega t+\varphi)$$
再求導得到加速度：
$$a=\frac{\mathrm{d}v}{\mathrm{d}t}=-A\omega^2\sin(\omega t+\varphi)$$
由$F=ma=-kx$可得方程：
$$-kx=mA\omega^2\sin(\omega t+\varphi)=-m\omega^2x$$
解得$\omega=\sqrt{k/m}$，又由$T=2\pi/\omega$，得：
$$T=2\pi\sqrt{\frac{m}{k}}$$

第二種推導方法

簡諧運動能量不變，因此使用能量法也很方便。
根據能量守恆，系統最大動能等於最大勢能：
$$E_{p\max}=E_{k\max}$$
同時根據$v=A\omega\cos(\omega t+\varphi)$，得到$v_{\mathrm{max}}=A\omega$，代入得：
$$E_{p\max}=\frac{1}{2}mA^2\omega^2=E_{k\max}=\frac{1}{2}kA^2$$
直接求得$\omega$，之後同上。

第三種推導方法

經過一個巧妙的變換，可將簡諧運動與勻速圓周運動關聯，於是得到第三種推導方法。
考慮勻速圓周運動在豎直方向上的投影，可以證明其是簡諧運動：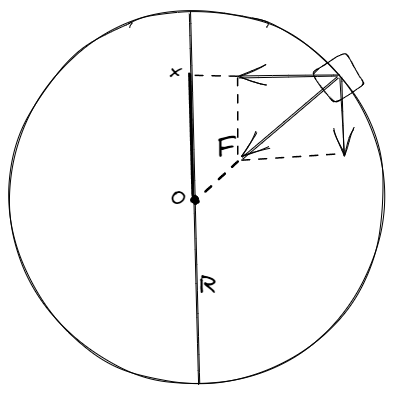

設物體與圓心連線同豎直方向的夾角為$\theta$，回復力$F’=F\cos\theta$，$x=R\cos\theta$，由於$F$和$R$是定值：
$$F’=\frac{F}{R}x=kx$$
所以勻速圓周運動在豎直方向上的投影是簡諧運動，同時該簡諧運動的周期即為勻速圓周運動周期。
當物體位移為$R$(在圓頂部)時，簡諧運動回復力恰等於向心力，可得$F=kR$，代入向心力公式得：
$$kR=m\omega^2R=m\frac{4\pi^2}{T^2}R$$
直接解方程即可得到：
$$T=2\pi\sqrt{\frac{m}{k}}$$

2. 推廣-阻尼振動

多數教輔上說阻尼振動周期大小不變，但有些地方又說周期大小增大。周期大小其實是近似推導得到的，而教輔上說「周期不變是因為其為固有屬性」是不正確的，阻尼振動的固有周期其實與無阻尼振動的不同。我讀了《振動力學(第三版)》的相關部分，簡記阻尼振動的周期推導過程如下。(抄書)

認為空氣阻力和液體潤滑界面阻力在物體運動速度不大時，近似與速度成正比，稱為黏性阻尼，阻力表示為$F_d=c\dot{x}$，$c$為黏性阻尼系數。據此可以直接寫出振動方程：
$$m\ddot{x}+c\dot{x}+kx=0$$
各項除以$m$，即可化成阻尼自由振動的標准形式：
$$\ddot{x}+2\zeta\omega_n\dot{x}+\omega_n^2x=0$$
其中$\omega_n$是無阻尼系統的固有角頻率，系數$\zeta$表征阻尼強弱，稱為阻尼比，分別定義為：
$$\omega_n=\sqrt{\frac{k}{m}},\quad\zeta=\frac{c}{2\sqrt{km}}$$
根據常微分方程理論，將特解$x=e^{\lambda t}$代入方程可得特征方程：
$$\lambda^2+2\zeta\omega_n\lambda+\omega_n^2=0$$
於是解出特征解：
$$\lambda_{1,2}=-(\zeta\mp\sqrt{\zeta^2-1})\omega_n$$

接下來分三種情況討論。
當$\zeta<1$時為欠阻尼狀態，方程通解為：
$$x=e^{-\zeta\omega_n t}(C_1\cos\omega_d t+C_2\sin\omega_d t)$$
也可以寫作：
$$x=Ae^{-\zeta\omega_n t}\sin(\omega_d t+\theta)$$
圖像大致如下：

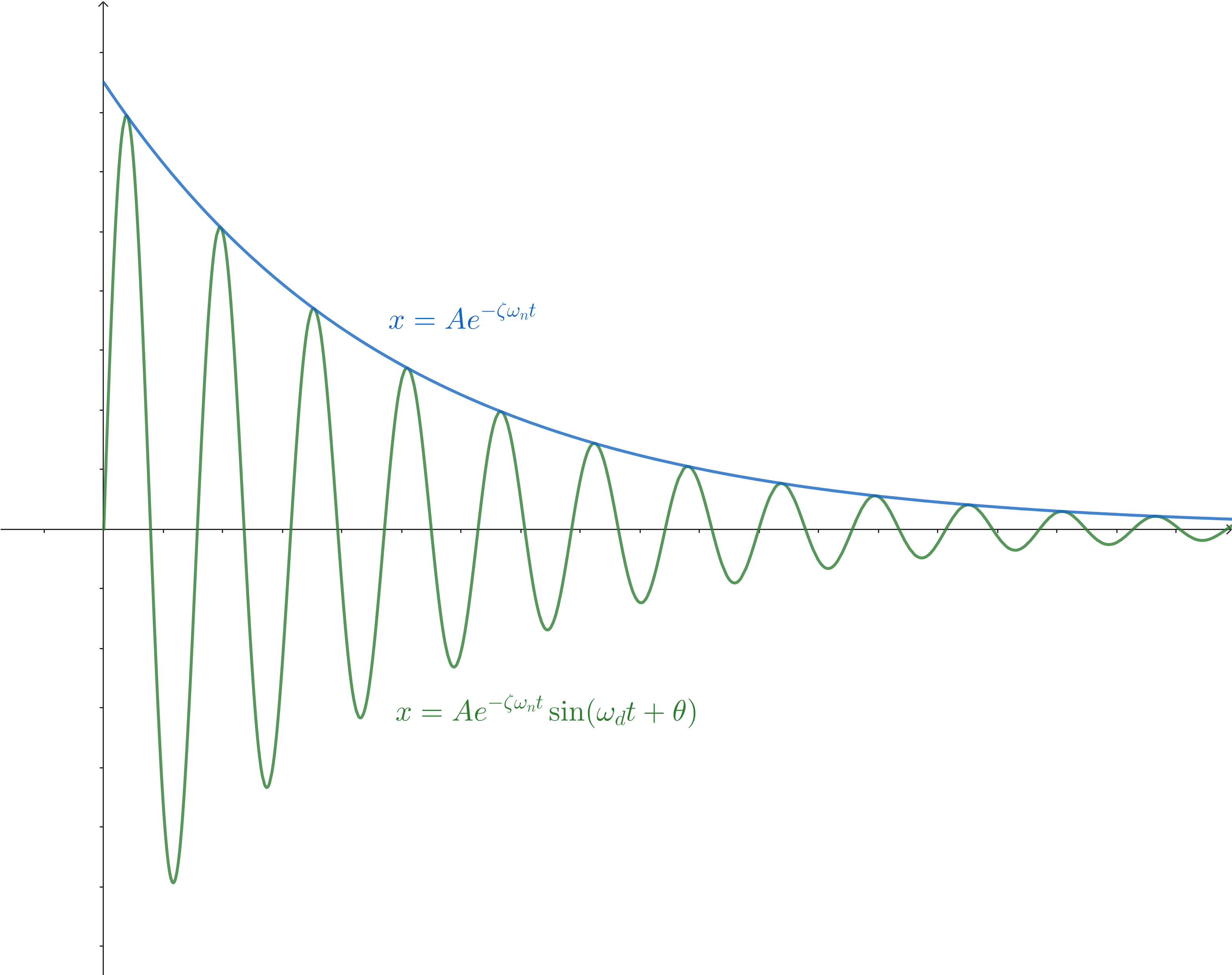
可以看到振動圖像具有包絡線，振幅以exp函數的形式衰減，但周期不隨時間變化。
式中$A$和$\theta$分別是初始幅值和初相角，由初始條件確定，具體不多贅述。重點是$\omega_d$，其為阻尼振動的固有角頻率，不隨時間變化，但小於無阻尼振動的固有角頻率$\omega_n$，表示為：
$$\omega_d=\omega_n\sqrt{1-\zeta^2}$$
由此可得阻尼振動的固有周期，大於無阻尼振動的固有周期：
$$T_d=\frac{2\pi}{\omega_d}=\frac{T_n}{\sqrt{1-\zeta^2}}$$
此外衰減振動的相鄰振幅之比也是常數(exp函數的性質)，稱為減縮因數$\eta$
當$\zeta>1$為過阻尼狀態，運動失去往復性，成為衰減的非往復運動。
當$\zeta=1$則為介於前兩種狀態之間的臨界狀態。

以上只是簡略的討論，具體參見《振動力學》。

3. 小角度單擺

忽略空氣阻力等因素，擺動角度極小的單擺可以看作簡諧運動，如圖：

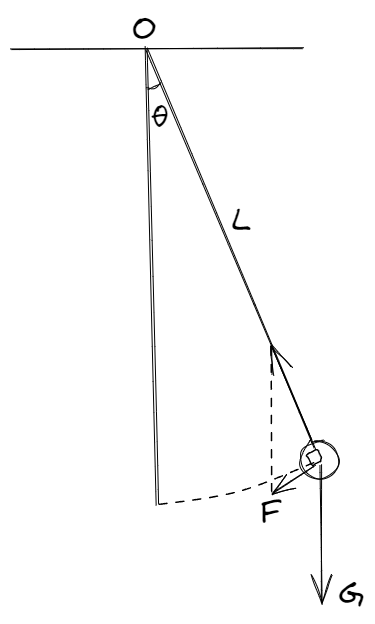
位移$x=L\theta$；因為物體所受合外力與運動軌跡相切，所以$F=-mg\sin\theta$，由於$\lim_{\theta\to0}\sin\theta=\theta$，所以近似地$F=-mg\theta$，於是：
$$k=-\frac{F}{x}=\frac{mg}{L}$$
代入簡諧運動周期公式可得單擺運動周期：
$$T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{L}{g}}$$

4. 推廣-一般的單擺

只有擺動角度極小的單擺可以看作簡諧運動，對於角度較大的單擺，情況會復雜許多，其周期甚至不能用基礎函數表示。
忽略空氣阻力等因素，取物理符號同上，則運動方程為：
$$mL\ddot{\theta}=-mg\sin\theta$$
從這個方程可知，周期與物體質量無關。但這個方程不好求解，於是換個角度，從能量守恆入手，設$\theta$角的最大值為$\theta_0$，在下落過程中，重力勢能轉化為動能，得到：
$$\frac{1}{2}mv^2=\frac{1}{2}m(\frac{\mathrm{d}\theta}{\mathrm{d}t})^2=mgh=mgl(\cos\theta-\cos\theta_0)$$
化簡，並取倒數得：
$$\frac{\mathrm{d}t}{\mathrm{d}\theta}=\frac{1}{\sqrt{2}}\sqrt{\frac{L}{g}}\frac{1}{\sqrt{\cos\theta-\cos\theta_0}}$$
因為$T=\theta_0\to0\to-\theta_0\to0\to\theta_0=4(\theta_0\to0)$，所以：
$$T=4\frac{1}{\sqrt{2}}\sqrt{\frac{L}{g}}\int_{0}^{\theta_0}\frac{1}{\sqrt{\cos\theta-\cos\theta_0}}\mathrm{d}\theta$$
這個積分不能用基礎函數表示，但可以表示為第一類橢圓積分：
$$T=4\sqrt{\frac{L}{g}}F(\sin\frac{\theta_0}{2},\frac{\pi}{2})$$
其中：
$$F(k,\phi)=\int_{0}^{\phi}\frac{1}{\sqrt{1-k^2\sin^2\theta}}\mathrm{d}\theta$$
參考Wikipedia
(話說最近老是遇到橢圓積分，打算有空了就研究一下這個。)