简谐运动与单摆周期

1. 简谐运动

第一种推导方法

设弹簧劲度系数为$k$，简谐运动位移方程为：
$$x=A\sin(\omega t+\varphi)$$
直接求导得速度：
$$v=\frac{\mathrm{d}x}{\mathrm{d}t}=A\omega\cos(\omega t+\varphi)$$
再求导得到加速度：
$$a=\frac{\mathrm{d}v}{\mathrm{d}t}=-A\omega^2\sin(\omega t+\varphi)$$
由$F=ma=-kx$可得方程：
$$-kx=mA\omega^2\sin(\omega t+\varphi)=-m\omega^2x$$
解得$\omega=\sqrt{k/m}$，又由$T=2\pi/\omega$，得：
$$T=2\pi\sqrt{\frac{m}{k}}$$

第二种推导方法

简谐运动能量不变，因此使用能量法也很方便。
根据能量守恒，系统最大动能等于最大势能：
$$E_{p\max}=E_{k\max}$$
同时根据$v=A\omega\cos(\omega t+\varphi)$，得到$v_{\mathrm{max}}=A\omega$，代入得：
$$E_{p\max}=\frac{1}{2}mA^2\omega^2=E_{k\max}=\frac{1}{2}kA^2$$
直接求得$\omega$，之后同上。

第三种推导方法

经过一个巧妙的变换，可将简谐运动与匀速圆周运动关联，于是得到第三种推导方法。
考虑匀速圆周运动在竖直方向上的投影，可以证明其是简谐运动：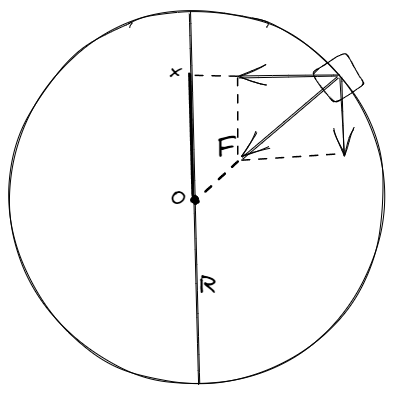

设物体与圆心连线同竖直方向的夹角为$\theta$，回复力$F’=F\cos\theta$，$x=R\cos\theta$，由于$F$和$R$是定值：
$$F’=\frac{F}{R}x=kx$$
所以匀速圆周运动在竖直方向上的投影是简谐运动，同时该简谐运动的周期即为匀速圆周运动周期。
当物体位移为$R$(在圆顶部)时，简谐运动回复力恰等于向心力，可得$F=kR$，代入向心力公式得：
$$kR=m\omega^2R=m\frac{4\pi^2}{T^2}R$$
直接解方程即可得到：
$$T=2\pi\sqrt{\frac{m}{k}}$$

2. 推广-阻尼振动

多数教辅上说阻尼振动周期大小不变，但有些地方又说周期大小增大。周期大小其实是近似推导得到的，而教辅上说“周期不变是因为其为固有属性”是不正确的，阻尼振动的固有周期其实与无阻尼振动的不同。我读了《振动力学(第三版)》的相关部分，简记阻尼振动的周期推导过程如下。(抄书)

认为空气阻力和液体润滑界面阻力在物体运动速度不大时，近似与速度成正比，称为黏性阻尼，阻力表示为$F_d=c\dot{x}$，$c$为黏性阻尼系数。据此可以直接写出振动方程：
$$m\ddot{x}+c\dot{x}+kx=0$$
各项除以$m$，即可化成阻尼自由振动的标准形式：
$$\ddot{x}+2\zeta\omega_n\dot{x}+\omega_n^2x=0$$
其中$\omega_n$是无阻尼系统的固有角频率，系数$\zeta$表征阻尼强弱，称为阻尼比，分别定义为：
$$\omega_n=\sqrt{\frac{k}{m}},\quad\zeta=\frac{c}{2\sqrt{km}}$$
根据常微分方程理论，将特解$x=e^{\lambda t}$代入方程可得特征方程：
$$\lambda^2+2\zeta\omega_n\lambda+\omega_n^2=0$$
于是解出特征解：
$$\lambda_{1,2}=-(\zeta\mp\sqrt{\zeta^2-1})\omega_n$$

接下来分三种情况讨论。
当$\zeta<1$时为欠阻尼状态，方程通解为：
$$x=e^{-\zeta\omega_n t}(C_1\cos\omega_d t+C_2\sin\omega_d t)$$
也可以写作：
$$x=Ae^{-\zeta\omega_n t}\sin(\omega_d t+\theta)$$
图像大致如下：

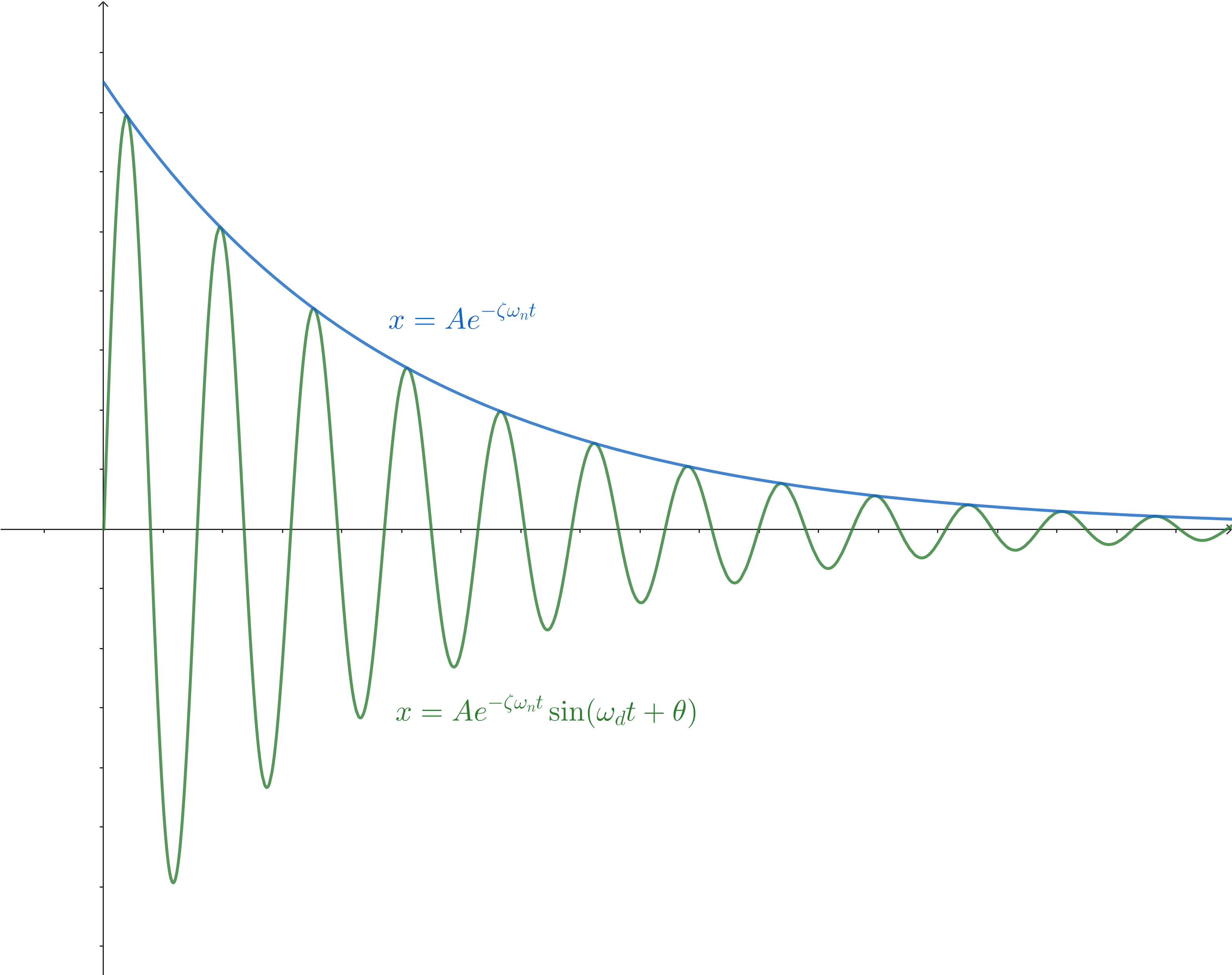
可以看到振动图像具有包络线，振幅以exp函数的形式衰减，但不随时间变化。
式中$A$和$\theta$分别是初始幅值和初相角，由初始条件确定，具体不多赘述。重点是$\omega_d$，其为阻尼振动的固有角频率，不随时间变化，但小于无阻尼振动的固有角频率$\omega_n$，表示为：
$$\omega_d=\omega_n\sqrt{1-\zeta^2}$$
由此可得阻尼振动的固有周期，大于无阻尼振动的固有周期：
$$T_d=\frac{2\pi}{\omega_d}=\frac{T_n}{\sqrt{1-\zeta^2}}$$
此外衰减振动的相邻振幅之比也是常数(exp函数的性质)，称为减缩因数$\eta$
当$\zeta>1$为过阻尼状态，运动失去往复性，成为衰减的非往复运动。
当$\zeta=1$则为介于前两种状态之间的临界状态。

以上只是简略的讨论，具体参见《振动力学》。

3. 小角度单摆

忽略空气阻力等因素，摆动角度极小的单摆可以看作简谐运动，如图：

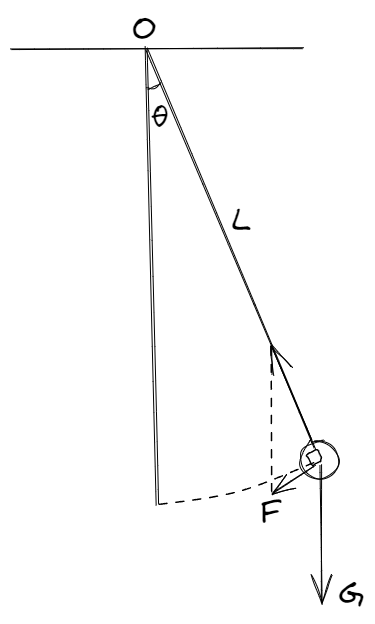
位移$x=L\theta$；因为物体所受合外力与运动轨迹相切，所以$F=-mg\sin\theta$，由于$\lim_{\theta\to0}\sin\theta=\theta$，所以近似地$F=-mg\theta$，于是：
$$k=-\frac{F}{x}=\frac{mg}{L}$$
代入简谐运动周期公式可得单摆运动周期：
$$T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{L}{g}}$$

4. 推广-一般的单摆

只有摆动角度极小的单摆可以看作简谐运动，对于角度较大的单摆，情况会复杂许多，其周期甚至不能用基础函数表示。
忽略空气阻力等因素，取物理符号同上，则运动方程为：
$$mL\ddot{\theta}=-mg\sin\theta$$
从这个方程可知，周期与物体质量无关。但这个方程不好求解，于是换个角度，从能量守恒入手，设$\theta$角的最大值为$\theta_0$，在下落过程中，重力势能转化为动能，得到：
$$\frac{1}{2}mv^2=\frac{1}{2}m(\frac{\mathrm{d}\theta}{\mathrm{d}t})^2=mgh=mgl(\cos\theta-\cos\theta_0)$$
化简，并取倒数得：
$$\frac{\mathrm{d}t}{\mathrm{d}\theta}=\frac{1}{\sqrt{2}}\sqrt{\frac{L}{g}}\frac{1}{\sqrt{\cos\theta-\cos\theta_0}}$$
因为$T=\theta_0\to0\to-\theta_0\to0\to\theta_0=4(\theta_0\to0)$，所以：
$$T=4\frac{1}{\sqrt{2}}\sqrt{\frac{L}{g}}\int_{0}^{\theta_0}\frac{1}{\sqrt{\cos\theta-\cos\theta_0}}\mathrm{d}\theta$$
这个积分不能用基础函数表示，但可以表示为第一类椭圆积分：
$$T=4\sqrt{\frac{L}{g}}F(\sin\frac{\theta_0}{2},\frac{\pi}{2})$$
其中：
$$F(k,\phi)=\int_{0}^{\phi}\frac{1}{\sqrt{1-k^2\sin^2\theta}}\mathrm{d}\theta$$
参考Wikipedia
(话说最近老是遇到椭圆积分，打算有空了就研究一下这个。)