遞推關系求數列通項公式
1. 一階線性遞推
一階線性遞推指$a_{n+1}=f(a_n)$,其中$f$是線性函數的遞推關系,可以用待定系數法轉化為相關的等比數列,從而求通項公式。
待定系數法
設數列$\{a_n\}$滿足$a_{n+1}=pa_n+q$,其中$pq(p-1)\not=0$。
假設遞推公式可寫成$a_{n+1}+t=p(a_n+t)$的形式,解得$t=q/(p-1)$,於是可知數列$\{a_n+\frac{q}{p-1}\}$是等比數列,寫出該數列的通項公式,即可得到原數列通項公式。
不動點法
這種方法也可理解為尋找不動點的方法。
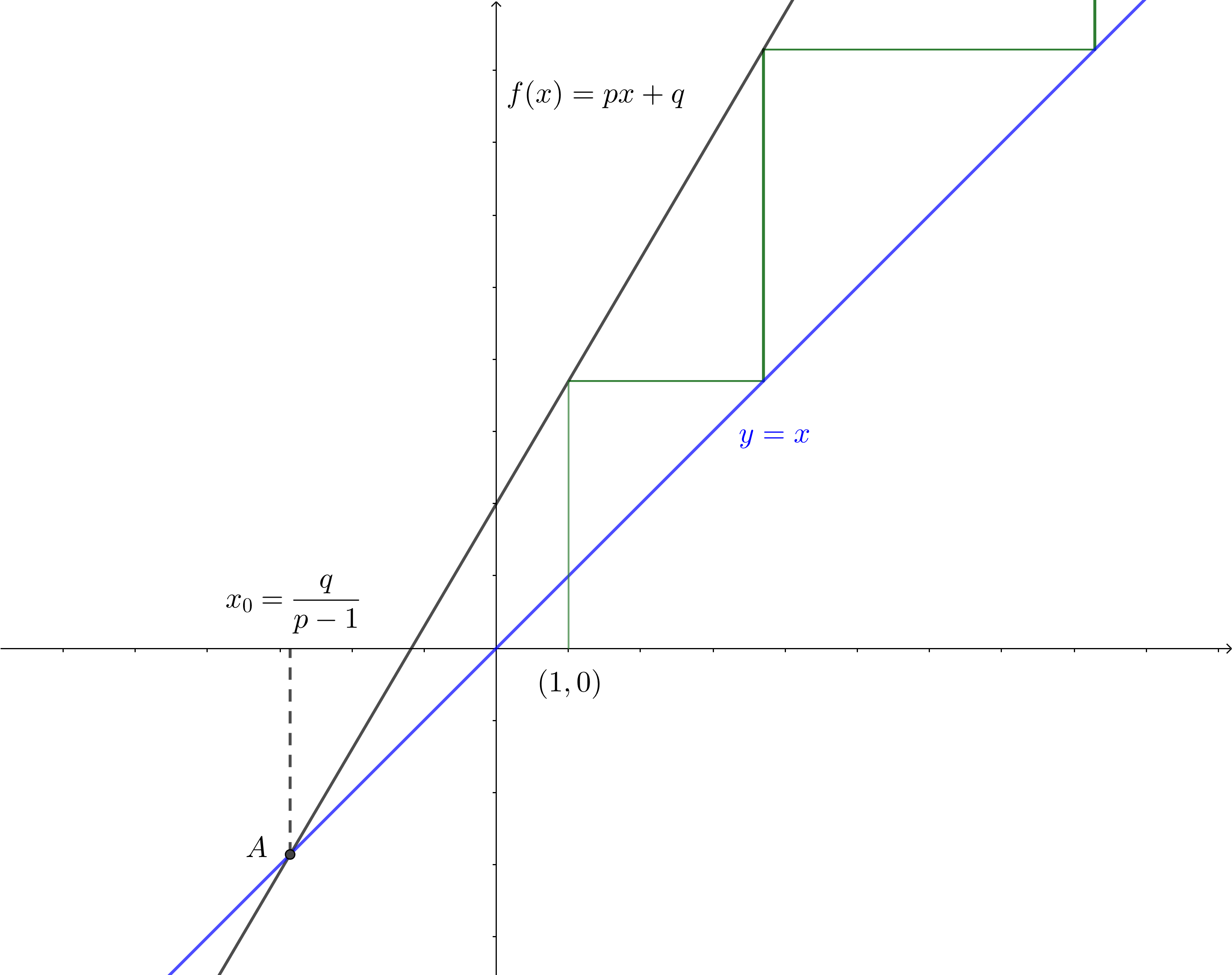
圖為遞推數列$\{a_n\}$的直觀表示,圖中折線為從點$(a_1,0)$開始的迭代,其與$f$交點的縱坐標恰為$a_2,a_3,a_4,\cdots,a_n$,$A$點是$f$與$y=x$的交點,這點的特殊之處是其在迭代之後仍是自身,因此被稱為不動點,而不動點外的任一點在迭代後都是發散的。
解方程$px+q=x$即可得到不動點的值,恰為$q/(p-1)$,與待定系數法中的$t$值相等,而之後的處理方法可以理解為將圖像整體向右上移動,使不動點與原點重合,得到的新數列$\{b_n\}$為等比數列,且$b_n=a_n+q/(p-1)$。顯然,只要$f(x)=px+q$,且$pq(p-1)\not=0$,則不動點必然存在。
若將遞推式稍加改動,變為$a_{n+1}=pa_n+qn+r$,不動點法就不適用了。但此數列顯然能表示為等比數列與一個確定的等差數列之和,可以使用待定系數法(本質其實差不多,可以認為存在一個規律變化的”不動點”)。
設$a_{n+1}+k(n+1)+l=p(a_n+kn+l)$,即:
$$
\begin{cases}
(p-1)k=q\\
pl-k-l=r
\end{cases}
$$
解得$k=q/(p-1)$,$l=r/(p-1)+q/(p-1)^2$,於是可知數列
$$\{a_n+\frac{q}{p-1}n+(\frac{r}{p-1}+\frac{q}{(p-1)^2})\}$$
是等比數列,之後的步驟同上。
2. 二階線性遞推
二階線性遞推指$a_{n+2}=f(a_{n+1})+g(a_n)$,其中$f,g$是線性函數的遞推關系,可以用待定系數法得到兩個相關的等比數列,原數列的每一項是兩個等比數列中對應項的線性組合。
待定系數法
先考慮最基本的情況,即$a_{n+2}=pa_{n+1}+qa_n$
假設$a_{n+2}-sa_{n+1}=t(a_{n+1}-sa_n)$,這樣設的目的是構造${a_n}$減去一個等比數列仍得到等比數列的形式。同時發現此式為對稱式,即可以改寫為$a_{n+2}-ta_{n+1}=s(a_{n+1}-ta_n)$的形式。
展開與原式比較可得方程組:
$$
\begin{cases}
s+t=p\\
st=-q
\end{cases}
$$
特征方程與特征根
根據韋達定理,$s,t$對應二次方程$x^2-px-q=0$的兩個根,該二次方程即數列的特征方程,$s,t$為特征根,因此該方法也被稱為特征根法。
接下來分兩種情況考慮。
若$s=t$,即$a_{n+2}-sa_{n+1}=s(a_{n+1}-sa_n)$,直接用累乘得$a_{n+2}=s^n(a_2-sa_1)+sa_{n+1}$,同理可得:
$$
\begin{align*}
sa_{n+1}&=s^n(a_2-sa_1)+s^2a_n\\
s^2a_n&=s^n(a_2-sa_1)+s^3a_{n-1}\\
&\cdots\cdots\\
s^{n-1}a_3&=s^n(a_2-sa_1)+s^na_2
\end{align*}
$$
於是再用累加,得到:
$$a_{n+2}=n\cdot s^n(a_2-sa_1)+s^na_2$$
即:
$$a_{n}=(n-2)\cdot s^{n-2}(a_2-sa_1)+s^{n-2}a_2$$
若$s\not=t$,將解得的$s,t$代回原式,並累乘(隨便改一下下標):
$$
\begin{align*}
a_{n+1}-sa_n&=t^{n-1}(a_2-sa_1)\\
a_{n+1}-ta_n&=s^{n-1}(a_2-ta_1)
\end{align*}
$$
兩式相減可得:
$$(t-s)a_n=t^{n-1}(a_2-sa_1)-s^{n-1}(a_2-ta_1)$$
於是得到通項公式:
$$a_n=\frac{1}{t-s}[t^{n-1}(a_2-sa_1)-s^{n-1}(a_2-ta_1)]$$
特別地,當$p=q=a_1=a_2=1$時,該數列為斐波那契數列,其特征根為:
$$
\begin{cases}
s=\frac{1-\sqrt{5}}{2}\\
t=\frac{1+\sqrt{5}}{2}
\end{cases}
$$
代入上式可得斐波那契數列通項公式:
$$a_n=\frac{1}{t-s}(t^{n}-s^{n})=\frac{\sqrt{5}}{5}\left[(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n\right]$$
復數根與周期性
若不存在實根,則必存在兩個不同的復根$s,t$,把它們代入上述公式,同樣能得到結果(上述推導過程換成復數也成立)。例如$a_{n+2}=a_{n+1}-a_n,a_1=1,a_2=2$,其特征方程為$x^2-x+1=0$,解得$s,t=(1\pm\sqrt3\mathrm{i})/2$,代入得:
$$a_n=-\frac{\sqrt3\mathrm{i}}{3}\left[(\frac{1+\sqrt3\mathrm{i}}{2})^{n-1}(\frac{3+\sqrt{3}\mathrm{i}}{2})-(\frac{1-\sqrt3\mathrm{i}}{2})^{n-1}(\frac{3-\sqrt{3}\mathrm{i}}{2})\right]$$
計算該數列的前幾項,發現其為以$1,2,1,-1,-2,-1$為周期的周期性數列,顯然這樣的性質在特征根為實數的二階遞推數列中是不可能的。那麼,滿足什麼條件的數列有此性質呢?
設$s,t=r(\cos\theta\pm\mathrm{i}\sin\theta)$,代入,使用棣莫弗定理化簡得:
$$a_n=\frac{r^{n-2}}{\sin\theta}[a_2\sin(n-1)\theta-ra_1\sin(n-2)\theta]$$
然後一個含復數的式子就直接轉換成了一個簡單的三角函數,用該式計算$a_n$:
$$
\begin{align*}
a_3&=\frac{r}{\sin\theta}(a_2\sin2\theta-ra_1\sin\theta)\\
a_4&=\frac{r^2}{\sin\theta}(a_2\sin3\theta-ra_1\sin2\theta)\\
a_5&=\frac{r^3}{\sin\theta}(a_2\sin4\theta-ra_1\sin3\theta)\\
&\cdots\cdots
\end{align*}
$$
於是可得,若數列存在周期性,顯然必須滿足兩點:
- 特征根的模長$r=1$
- 輻角$\theta=p\pi/q$,其中$p,q\in\mathbb{Z}\backslash0$
滿足這兩點後,數列必為周期數列,且可以確定周期長度為$(p+1)\cdot(q,2)$
對於$a_{n+2}=pa_{n+1}+qa_n+r$或$a_{n+2}=pa_{n+1}+qa_n+rn+s$這樣更復雜的遞推關系,其本質也是兩個等比數列的線性組合,只是添加常數項或確定的等差數列項,在此限於篇幅,不多贅述。
3. $k$階線性遞推
對於$k$階線性遞推,即表示為$a_{n+k}=c_1a_{n+k-1}+c_2a_{n+k-2}+\cdots+c_ka_n,k\ge2$的遞推關系,情況要復雜很多,很明顯初等數學不夠用了。
用矩陣來表示遞推關系,那麼斐波那契數列就可表示為:
$$\begin{bmatrix}a_{n+1}\\a_{n}\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}\begin{bmatrix}a_{n}\\a_{n-1}\end{bmatrix}$$
則可以直接乘起來得到通項公式:
$$\begin{bmatrix}a_{n+1}\\a_{n}\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}^n\begin{bmatrix}1\\1\end{bmatrix}$$
同樣的,$k$階線性遞推通項公式可用矩陣表示為:
$$\begin{bmatrix}a_{n}\\a_{n-1}\\\cdots\\a_{n-k+2}\\a_{n-k+1}\end{bmatrix}=\begin{bmatrix}c_1&c_2&\cdots&c_{k-1}&c_k\\1&0&\cdots&0&0\\0&1&\cdots&0&0\\\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&\cdots&0&0\\0&0&\cdots&1&0\end{bmatrix}^{n-1}\begin{bmatrix}a_{k}\\a_{k-1}\\\cdots\\a_{2}\\a_{1}\end{bmatrix}$$
理論上求出上式中$k\times k$矩陣的$n$次冪就能得到通項公式,但實際上根本不會算,等我有時間學了線性代數在補吧。
4. 分式遞推
取倒
對於分子無常數項的分式遞推數列,直接兩邊取倒數即可。
遞推關系(注意遞推式函數圖像經過原點)
$$a_n=\frac{pa_{n-1}}{qa_{n-1}+r}$$
取倒數得:
$$\frac{1}{a_n}=\frac{q}{p}\cdot\frac{1}{a_{n-1}}+\frac{r}{p}$$
於是得到一階線性遞推數列$\{1/a_n\}$,用待定系數法求出其通項公式,再取其倒數就得到原數列通項公式。
不動點法
對於一般形式的分式遞推數列,即$x_n=(ax_{n-1}+b)/(cx_{n-1}+d)$的遞推關系,可以使用不動點方法。
有了一階線性遞推的經驗,就直接解方程:
$$\frac{ax+b}{cx+d}=x$$
即方程$cx^2+(d-a)x-b$,該方程也稱作此分式遞推數列的特征方程,其根同樣可稱為特征根。
解這個二次方程可以得到2個根,分兩種情況考慮。
若$x_1=x_2=\alpha$,則數列有一個不動點。在遞推式兩邊同時減去$\alpha$再取倒數,可得到一個相關的等差數列,求出該數列通項公式後稍作處理可得原數列通項公式。這裡的一個問題是,為什麼得到的是相關的等差數列,而不是一般的一階線性遞推數列?
對於此問題,有一種直觀的理解方法。像本文一開始那樣用圖像表示遞推過程:
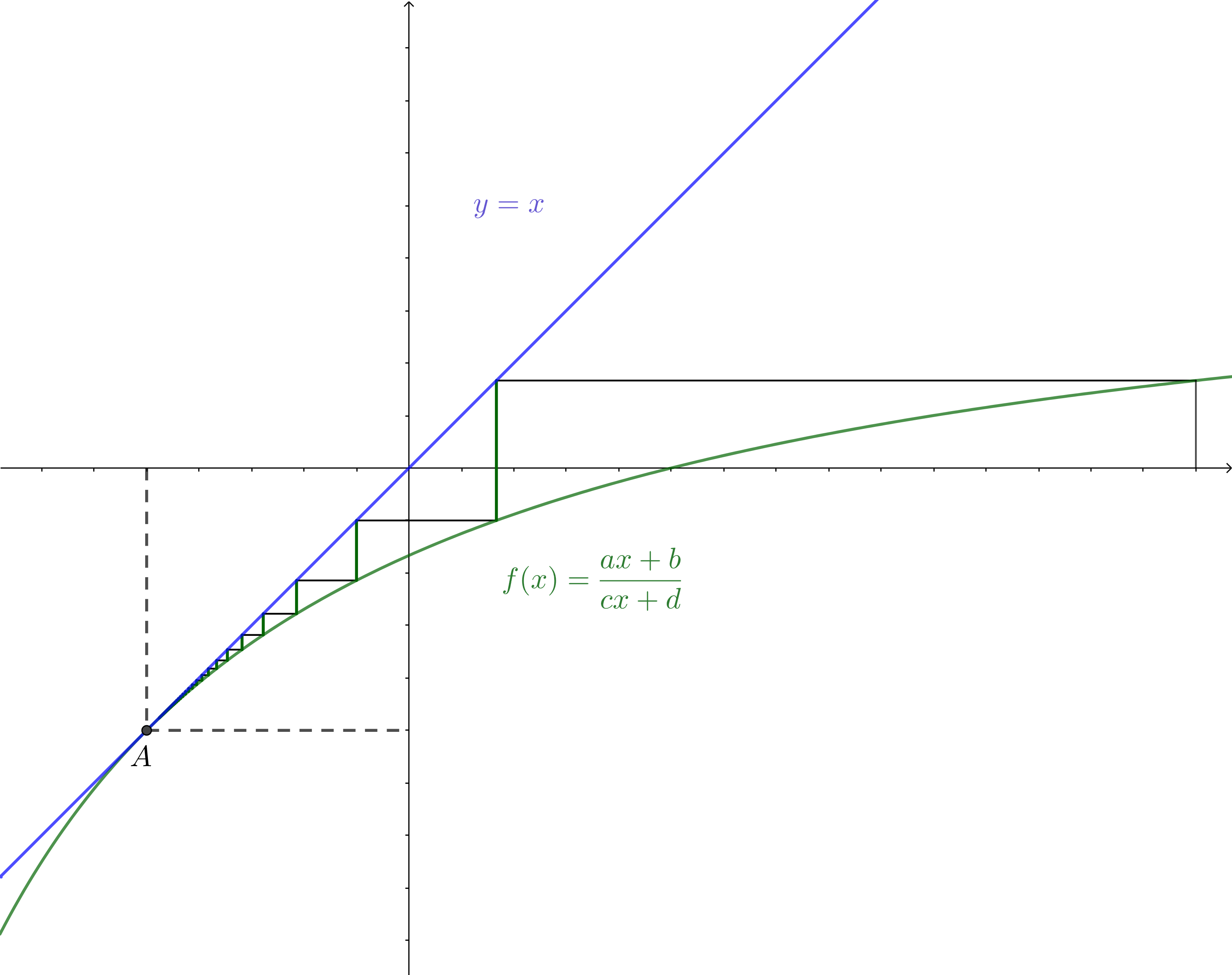
如圖,$A$即為不動點,其坐標$(\alpha,\alpha)$,$f$與$y=x$在$A$點相切。在遞推公式兩邊減去$\alpha$,就相當於將整個圖像向右上平移,使$A$與原點重合。於是該數列就轉化為一個可以直接取倒數求解的簡單分式遞推數列(遞推式函數圖像經過原點),同時還滿足圖像在原點處與$y=x$相切。所以只需證滿足以上兩個條件的函數取倒數後$-1$次項系數為$1$,即:
$$
\begin{cases}
g(x)=\frac{px}{qx+r}\\
g’(0)=1
\end{cases}
\Rightarrow \frac{1}{g(x)}=\frac{1}{x}+\lambda
$$
其中$p,q,r,\lambda$是常數。這是容易證明的,具體過程就不寫了。
但這好像有些兜圈子了,更「簡單」的方法是直接把$\alpha=(a-d)/2c$代進去計算,這樣甚至能把得到的等差數列的公差算出來。懶得計算了,就直接寫最終結論吧,該等差數列遞推公式為:
$$\frac{1}{x_{n}-\alpha}=\frac{1}{x_{n-1}-\alpha}+\frac{2c}{a+d}$$
例如,$x_n=(x_{n-1}-1)/(x_{n-1}+3)$,其特征方程$x^2+2x+1=0$,解得$x_1=x_2=-1$,於是變換遞推式為:
$$x_n+1=\frac{x_{n-1}-1}{x_{n-1}+3}+1=\frac{2x_{n-1}+2}{x_{n-1}+3}$$
兩邊取倒數得:
$$\frac{1}{x_n+1}=\frac{1}{x_{n+1}+1}+\frac{1}{2}$$
若$x_1=\beta_1\not=x_2=\beta_2$,則數列有兩個不動點。分別將遞推公式減去兩個不動點,得到兩個式子:
$$
\begin{align*}
x_n-\beta_1=\frac{ax_{n-1}+b}{cx_{n-1}+d}-\beta_1=\frac{(a-\beta_1c)(x_{n-1}-\beta_1)}{cx_{n-1}+d}\\
x_n-\beta_2=\frac{ax_{n-1}+b}{cx_{n-1}+d}-\beta_2=\frac{(a-\beta_2c)(x_{n-1}-\beta_2)}{cx_{n-1}+d}
\end{align*}
$$
兩式相除得到:
$$\frac{x_n-\beta_1}{x_n-\beta_2}=\frac{a-\beta_1c}{a-\beta_2c}\cdot\frac{x_{n-1}-\beta_1}{x_{n-1}-\beta_2}$$
得到一個相關的等比數列,略加處理即可得到原數列通項公式。
例如,$x_n=(x_{n-1}-2)/(x_{n-1}+4)$,其特征方程$x^2+3x+2=0$,解得$x_1=-1,x_2=-2$,代入得到兩個式子:
$$
\begin{align*}
x_n+1=\frac{2x_{n-1}+2}{x_{n-1}+4}\\
x_n+2=\frac{3x_{n-1}+6}{x_{n-1}+4}
\end{align*}
$$
兩式相除得到:
$$\frac{x_n+1}{x_n+2}=\frac{2}{3}\cdot\frac{x_{n-1}+1}{x_{n-1}+2}$$
以上就是基本的不動點法,事實上,題目中還可能出現高次的分式遞推,本質也是用上述方法,但需要一些額外的處理,具體情況具體分析。
復數根與周期性
如果分式遞推數列特征根是復數,那麼不動點就不存在了。正如在二階線性遞推部分所討論的,可以將復根代入公式,不影響最終結果。那麼就產生了一個問題:這樣的情況下該分式遞推數列是否可能是周期數列?
不妨先看一下一些不動點不存在的分式數列迭代圖像:
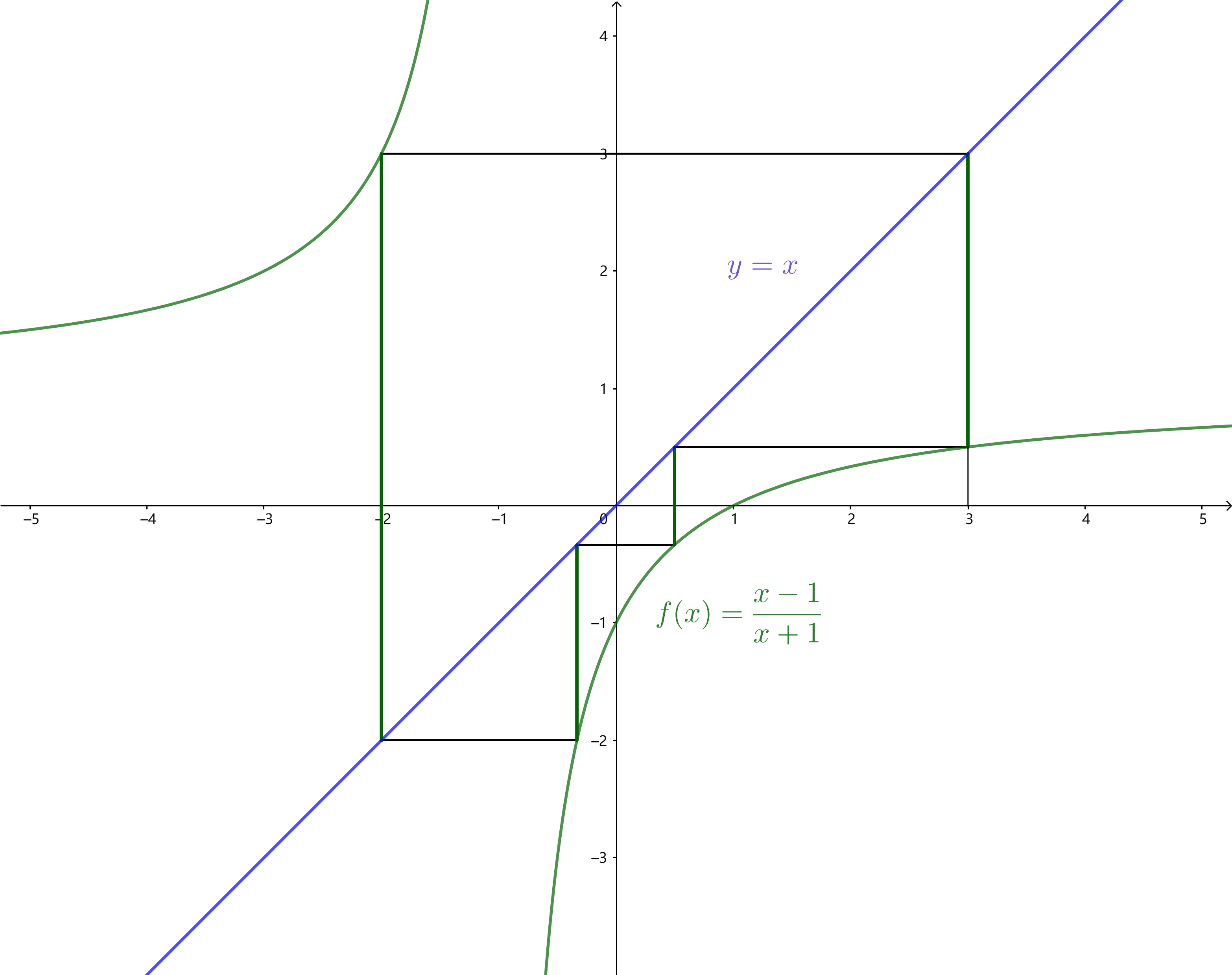
遞推公式:$a_n=(a_{n-1}-1)/(a_{n-1}+1)$
特征根:$x_1=\mathrm{i},x_2=-\mathrm{i}$
是周期性數列,其周期是$8$
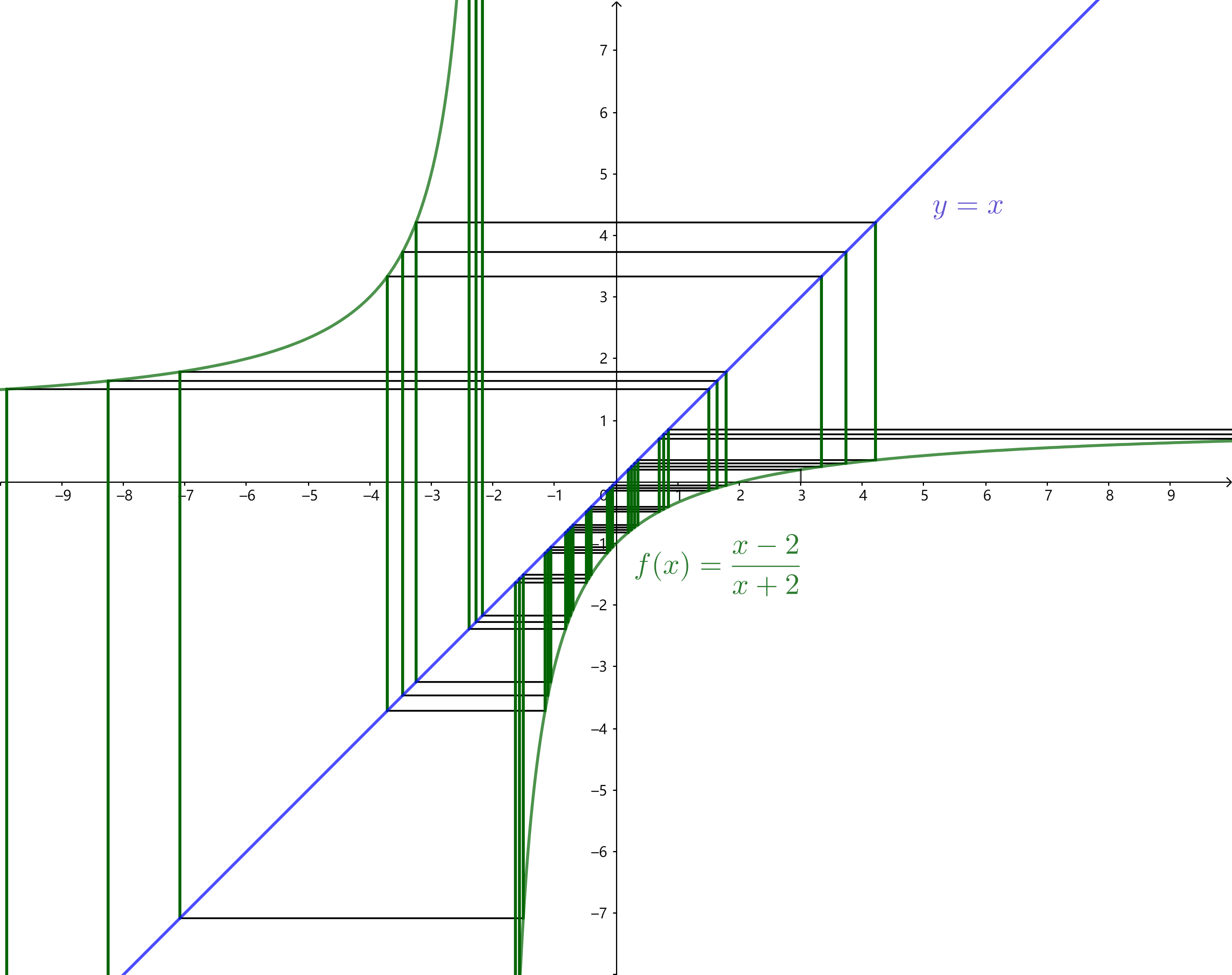
遞推公式:$a_n=(a_{n-1}-2)/(a_{n-1}+2)$
特征根:$x_1=(-1+\sqrt{7}\mathrm{i})/2,x_2=(-1-\sqrt{7}\mathrm{i})/2$
顯然不是周期性數列,迭代值不斷「震蕩」,但不會重復,應該可以迭代到函數上每一點。
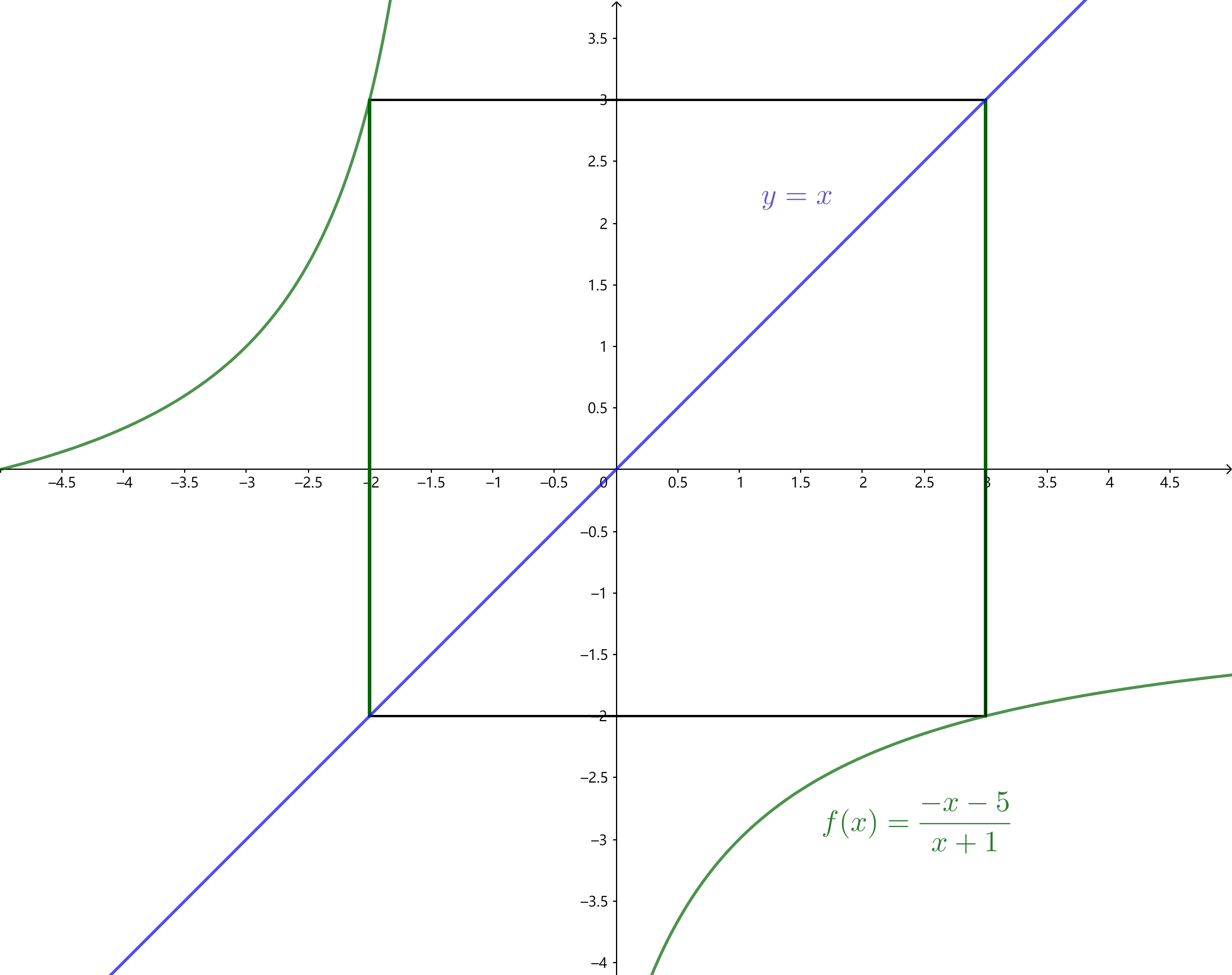
遞推公式:$a_n=(-a_{n-1}-5)/(a_{n-1}+1)$
特征根:$x_1=-1+2\mathrm{i},x_2=-1-2\mathrm{i}$
是周期性數列,其周期為$4$
看到以上三個例子,就基本能總結規律了。與二階線性遞推中對特征根模長與輻角的要求不同,這裡的要求是復根的實部和虛部都為有理數。這樣,對初始值進行迭代就終將回歸自身,形成周期,否則會會迭代到函數上的每一點。當然,以上僅為猜想,並沒有證明,等有時間了再研究一下這個問題。
5. 特殊處理
上面說的全都是套路性的方法,實際的數列題當然不可能這麼簡單,一般需要對非線性的遞推式進行特殊處理。下面舉兩道例題。
例1:$a_1=a_2=1$,$a_n=(a_{n-1}^2+2)/a_{n-2}$,求通項公式。
又是二階又是分式遞推,還是二次的,完全沒有頭緒。那就憑感覺化簡一下,第一步先把分子乘過去,使兩邊齊次:
$$a_na_{n-2}=a_{n-1}^2+2$$
然後再寫一項:
$$a_{n+1}a_{n-1}=a_{n}^2+2$$
兩式相減消去常數項:
$$a_{n+1}a_{n-1}-a_na_{n-2}=a_n^2-a_{n-1}^2$$
這樣,式子的項數反而增加到了4項,但還是沒有明顯的規律。繼續化簡,整理一下,提取公因數:
$$a_n(a_n+a_{n-2})=a_{n-1}(a_{n+1}+a_{n-1})$$
居然直接就配成常數列了,但下標不連續很不方便,於是把括號除到另一半得到:
$$\frac{a_n}{a_{n+1}+a_{n-1}}=\frac{a_{n-1}}{a_n+a_{n-2}}=\frac{a_2}{a_3+a_1}=\frac{1}{4}$$
於是可知$4a_n=a_{n+1}+a_{n-1}$,接下來按照二階線性遞推的方法計算即可。
例2:$x_0=0$,$x_{n+1}=3x_n+\sqrt{8x_n^2+1}$,求通項公式。
還是往齊次去湊,把$3x_n$移到左邊,兩邊平方得到方程:
$$x_{n+1}^2-6x_nx_{n+1}+x_n^2-1=0$$
這是個對稱式,所以再寫一項:
$$x_{n-1}^2-6x_nx_{n-1}+x_n^2-1=0$$
於是可知$x_{n+1},x_{n-1}$恰為$x^2-6x_nx+x_n^2-1=0$的兩根,根據韋達定理:
$$x_{n+1}+x_{n-1}=6x_n$$
接下來按照二階線性遞推的方法計算即可。
所有形如$x_{n+1}=ax_n+\sqrt{(a^2-1)x_n^2+b}$的遞推數列都可用此方法求通項公式。
這個例題比較有意思的一點是,數列中每一項都是整數。如果遞推公式的系數$a,b$發生改變,就不一定存在這樣全為整數的數列了,改變迭代的初始值,得到的也不一定是這樣的數列。那麼整數數列與遞推公式的系數和迭代初始值有什麼關系呢?這又是一個有意思的問題。(這個形式讓我想起了拉馬努金恆等式,但也許沒什麼關聯?)