群论学习笔记-5.群的陪集分解
直观理解
观察一个群的凯莱图,容易发现它的一个子群的结构在整个群中反复出现。例如群$G=S_3$,其中子群$H=C_2=\{e,f\}$的结构出现3次: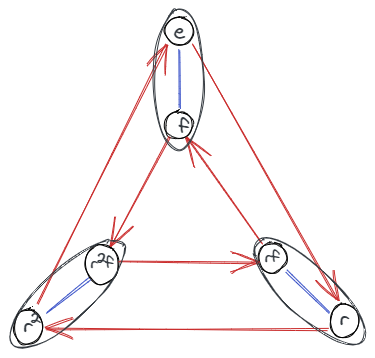
这3个相同的结构称为$H$在群$G$中的陪集,更准确地说是左陪集,分别表示为$eH=e\langle f\rangle=\{e,f\}$, $rH=r\langle f\rangle=\{r,rf\}$ 和 $r^2H=r^2\langle f\rangle=\{r^2,r^2f\}$。
类似的情况在各群中都存在,用$aH$来表示子群$H$的左陪集,即$H$中各元素左乘$a$得到的集合。陪集的存在是可以由凯莱图的同质性(Homogeneity)确保,详见群论学习笔记-1.群的概念#凯莱图 (Visual Group Theory中称正则性Regular,但图论中正则性另有所指,于是改用Tao的文章中的术语)。
除左陪集之外,也存在右陪集$Ha$,即$H$中各元素右乘$a$得到的集合。在上面的凯莱图中,左陪集保留了原子群的结构,而右陪集却很分散,原因是规定箭头的方向是左乘,如果规定方向为右乘,则情况恰恰相反。左右陪集一般不相等,满足对任意元素$g$,$gH=Hg$的特殊子群称为正规子群,是重要的研究对象。
左右陪集的许多性质是相同的。观察凯莱图,得到以下结论(后文将用代数方法证明):
- 若元素$b\in aH$,则$aH=bH$,类似结论对右陪集也成立。
- 一个群的任意子群都有陪集,且这些陪集恰覆盖群中所有元素,或者说,任意子群的陪集恰划分这个群。
代数定义
设$H$是群$G$的子群,将$H$中所有元素右乘$g$得到的集合称为$H$在$G$中的一个右陪集,记为:
$$Ha=\{xa\mid x\in H\}$$
类似的,有左陪集:
$$aH=\{ax\mid x\in H\}$$
例如,整数加法群中所有7的倍数构成一个子群$7\mathbb{Z}$,它的陪集(左右陪集相等)可表示为:
$$i+7\mathbb{Z}=\{i,i\pm7,i\pm14,i\pm21\cdots\},\quad i=1,2,\cdots,6$$
且容易看出:
$$\mathbb{Z}=7\mathbb{Z}\cup(1+7\mathbb{Z})\cup(2+7\mathbb{Z})\cup\cdots\cup6+7\mathbb{Z}$$
性质
基本性质
$H$在$G$中的陪集有如下性质(仅讨论右陪集,结论对左陪集也成立):
- $Ha$中的元素个数与$H$中相等
- $H$本身是也一个陪集:$He=H$;$Ha=H$的充要条件是$a\in H$
- $a$在陪集$Ha$中($ea=a$),将$a$称为$Ha$的一个陪集代表
- 若元素$b\in Ha$,则$Ha=Hb$
证明:因为$b\in Ha$,所以有$h\in H$使$b=ha$,所以$Hb=Hha=Ha$ - $Ha=Hb\Leftrightarrow ab^{-1}\in H$
证明:使用消去律得到$Hab^{-1}=H$,由性质2得到$ab^{-1}\in H$ - 任意两个陪集$Ha,Hb$,或者$Ha=Hb$,或者$Ha\cap Hb=\varnothing$
证明:若$Ha\cap Hb\not=\varnothing$,则存在$c\in Ha$且$c\in Hb$,由性质4可得$Ha=Hb$
由性质6可知$G$可被分解为多个不同的陪集的并:
$$G=Ha_1\cup Ha_2\cup\cdots\cup Ha_r$$
其中
$$Ha_i\cap Ha_j=\varnothing,\quad i,j=1,2,\cdots,r,\quad i\not=j$$
这个式子称为$G$的右陪集分解式。$r$是陪集的个数,称为$H$在$G$中的指数,记作$[G:H]$,$a_1,a_2,\cdots,a_r$称为$H$在$G$中的右陪集代表系。
陪集分解的性质
由上述陪集的性质可以得到两个重要的定理。
定理1(Lagrange定理):群$G$的阶等于子群$H$的阶及$H$在$G$中的指数的乘积,即:
$$|G|=|H|\cdot[G:H]$$
证明:设$G$的右陪集分解式为$G=Ha_1\cup Ha_2\cup\cdots\cup H_r$,则$|Ha_i|=|H|$,所以
$$|G|=|Ha_i|\cdot r=|H|\cdot[G:H]$$
推论:有限群$G$中每个元素的阶都是$G$的阶$|G|$的因子;若$G$的阶等于$n$,则$G$中任意元素$a$满足$a^n=e$
证明:设$a$是$G$中的一个$m$阶元素,则$H=\langle a\rangle$是$G$的一个子群,且$|H|=m$,由Lagrange定理,$m\mid |G|$。另一结论是显然的。
定理2:设$G\ge H\ge K$,则:
- $[G:K]=[G:H]\cdot[H:K]$
- 若$G$对$H$的陪集分解为$G=Hg_1\cup Hg_2\cup\cdots\cup Hg_l$
$H$对$K$的陪集分解为$H=Kh_1\cup Kh_2\cup\cdots\cup Kh_m$
则$G$对$K$的陪集分解为$G=\bigcup Kh_ig_j\quad(i=1,\cdots,m;j=1,\cdots,l)$ - 若$G$对$K$的陪集分解为$G=Ka_1\cup Ka_2\cup\cdots\cup Ka_t$
则可以调整$a$的顺序,使得$H=Ha_1=Ka_1\cup Ka_2\cup,\cdots,\cup Ka_m$,$\cdots$
$Ha_{m+1}=Ka_{m+1}\cup Ka_{m+2}\cup,\cdots,\cup Ka_{2m}$,$\cdots$
$Ha_{(l-1)m+1}=Ka_{(l-1)m+1}\cup Ka_{(l-1)m+2}\cup,\cdots,\cup Ka_{lm},\quad lm=t$
且$G$对$H$的陪集分解为$G=Ha_1\cup Ha_{m+1}\cup,\cdots,\cup Ha_{(l-1)m+1}$
证明:
- 因为$|G|=[G:H]\cdot|H|$,$|H|=[H:K]\cdot|K|$,所以$|G|=[G:H]\cdot[H:K]\cdot|K|$,原式得证
- 陪集$Kh_ig_j$共有$lm$个,与$K$在$G$中的指数相等,同时易证这些陪集两两不相交,于是定理得证
- 此为定理2的逆定理,证明略。
推论:设$G\ge H\ge K$,则:
- 若$g_1,g_2,\cdots,g_l$是$H$在$G$中的一个右陪集代表系,$h_1,h_2,\cdots,h_m$是$K$在$H$中的一个右陪集代表系,则$g_1h_1,\cdots,g_1h_m,\cdots,g_lh_1,\cdots,g_lh_m$是$K$在$G$中的一个右陪集代表系。特别地,取$g_1=e$,可知这个右陪集代表系中包含$h_1,h_2,\cdots,h_m$
- 在$G$对$K$的任一个右陪集代表系中,总能得到一部分组成$H$对$K$的任一个右陪集代表系中。
应用
接下来使用基本群论证明Fermat小定理。
定理:$a^{p-1}\equiv1\mod p$,其中$p$为素数,$a=1,2,\cdots,p-1$
证明:在集合$\{1,2,\cdots,p-1\}$中定义乘法$a\cdot b=r$,其中$r$为$p$除$ab$的余数。首先证明其满足群的定义:
- 封闭性:$(p,a)=(p,b)=1$,$p$除$ab$必得到$1$至$p-1$的余数。
- 单位元:存在单位元$1$
- 逆元:$\forall a,\exists b$,使得$ab\equiv1\mod p$,可用裴蜀定理证明。
由Lagrange定理得,群中任意元素的阶整除群的阶。这里群的阶是$p-1$,所以$a^{(p-1)/k}\equiv1\mod p$,其中$k$为一整数,于是根据同余的性质可得$a^{p-1}\equiv1\mod p$