van Roomen問題

1. 問題

400多年前，數學家Adriaan van Roomen以他的著作Ideae mathematicae中的一個45次方程向當時的歐洲頂尖數學家發起挑戰，而挑戰的名單中沒有法國數學家。荷蘭大使據此向法國國王指出：法國沒有頂尖數學家，於是法國國王召見François Viète (沒錯就是韋達定理的那個韋達)，讓他解這個方程。他靠著窗戶站了一會兒後就給出了一個解，並在第二天就給出了另外22個(正)解。

這個方程是這樣的^[1]：

用現代數學語言表示就是這樣一個多項式：
$$P_{45}(x)=45x-3795x^3+95634x^5-1138500x^7+7811375x^9-34512075x^{11}+105306075x^{13}-232676280x^{15}+384942375x^{17}-488494125x^{19}+483841800x^{21}-378658800x^{23}+236030652x^{25}-117679100x^{27}+46955700x^{29}-14945040x^{31}+3764565x^{33}-740259x^{35}+111150x^{37}-12300x^{39}+945x^{41}-45x^{43}+x^{45}$$
方程為：
$$P_{45}(x)=K=\sqrt{\frac{7}{4}-\sqrt{\frac{5}{16}}-\sqrt{\frac{15}{8}-\sqrt{\frac{45}{64}}}}$$

2. 試水

雖然是45次方程，但畢竟是400多年前的。
太簡單了！只要運用一下高科技，答案立即就出來了：

Ut legit, ut solvit !! 45個根，23個正根，22個負根，並且有20位的精度。

但是，這畢竟是400多年前的問題，使用計算機數值算法純屬犯規了。雖然沒必要像Viète一樣用紙筆解方程，還是讓我們來推測一下他的解題思路。
首先觀察$P_{45}$的這一堆系數。注意到系數的正負號是交替的，那麼基本可以斷定這個式子是某個函數的展開式，但是究竟是什麼函數呢？畫個圖像看看：

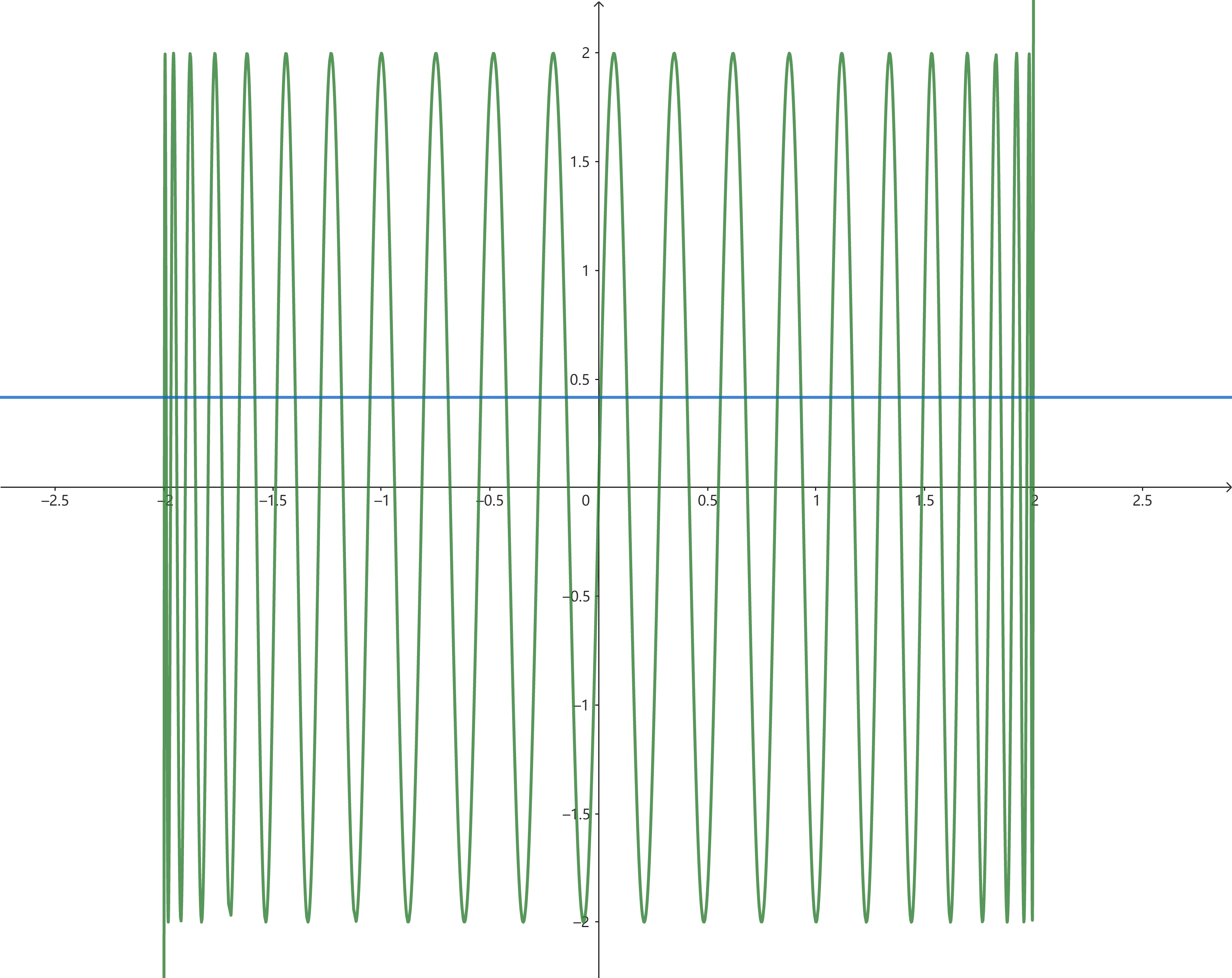
看到這個經典的波形，就知道這一定是某個三角函數了。這樣也就能解釋為什麼這個方程的45個根恰好都是實數了。關鍵問題就在於如何找到這個三角函數。
先把這一堆系數分解質因數：
$$
\begin{align*}
45&=3^2\times5\\
3795&=3\times5\times11\times23\\
95634&=2\times3^3\times7\times11\times23\\
1138500&=2^2\times3^2\times5^3\times11\times23\\
\cdots&\cdots\\
111150&=2\times3^2\times5^2\times13\times19\\
12300&=2^2\times3\times5^2\times41\\
945&=3^3\times5\times7\\
45&=3^2\times5
\end{align*}
$$
除了質因數大小在一定范圍內，似乎沒有什麼規律。

3. 正式解題

引入三角函數

查閱資料後我發現，這個問題竟與三次方程的三角解法有關。
考察沒有二次項的三次方程(Depressed Cubic Equation)，即形如$x^3+px+q=0(p,q\not=0)$的方程。Viète對其提出了一種利用三角函數的解法^[2]。

關鍵在於三倍角公式的運用：$4\sin^3\theta=3\sin\theta-\sin3\theta$
令$x=A\sin\theta$，$C=\sin3\theta$，代入三倍角公式：
$$4\left(\frac{x}{A}\right)^3=3\left(\frac{x}{A}\right)-C$$
化簡：
$$x^3-\frac{3}{4}A^2x+\frac{1}{4}A^3C=0$$
於是得到：
$$
\begin{cases}
p=-3A^2/4\\
q=A^3C/4
\end{cases}
$$
解這個方程組，得到：
$$
\begin{cases}
A=2\sqrt{-p/3}\\
C=\sin3\theta=4q/A^3=-9q/(2p\sqrt{-3p})
\end{cases}
$$
於是可以求出$\theta$的值^[3]：
$$\theta=\frac{1}{3}\arcsin\left(-\frac{9q}{2p\sqrt{-3p}}\right)+\frac{2k\pi}{3},\quad k=0,1,2$$
再代回$x=A\sin\theta$：
$$x=2\sqrt{-\frac{p}{3}}\cdot\sin\left(\frac{1}{3}\arcsin\left(-\frac{9q}{2p\sqrt{-3p}}\right)+\frac{2k\pi}{3}\right),\quad k=0,1,2$$
這個求根公式適用於任意無二次項的三次方程，用公式可求出方程的三個根($k=0,1,2$)。若規定$p<0$，$q<0$，則不等式$-1<-9q/(2p\sqrt{-3p})<1$恆成立，三個根都為實數。

順便一提，如果將$y=x-a/3$代入一般的三次方程$y^3+ay^2+by+c=0$，即可消去二次項，得到$x^3+(b-a^2/3)x+(2a^3/27-ab/3+c)=0$，因此這個三角函數解法可以直接應用於任意三次方程。

化簡多項式

可以使用相同的方法化簡$P_{45}$。
既然是45次，那就需要$\sin45\theta$，$45=3^2\times5$，那麼顯然需要使用一次五倍角公式和兩次三倍角公式。
$$\sin45\theta=16\sin^5 9\theta-20\sin^3 9\theta+5\sin 9\theta$$
$$\sin9\theta=-4\sin^3 3\theta+3\sin 3\theta$$
設$a=\sin3\theta$，則：
$$
\begin{aligned}
\sin45\theta&=16(-4a^3+3a)^5-20(-4a^3+3a)^3+5(-4a^3+3a)\\
&=-16384a^{15}+61440a^{13}-92160a^{11}+70400a^9-28800a^7+6048a^5-560a^3+15a
\end{aligned}
$$
設$b=\sin\theta$，則：
$$\sin45\theta=17592186044416 b^{45}-197912092999680 b^{43}+1039038488248320 b^{41}-3380998255411200 b^{39}+7638169839206400 b^{37}-12717552782278656 b^{35}+16168683558666240 b^{33}-16047114509352960 b^{31}+12604574741299200 b^{29}-7897310717542400 b^{27}+3959937231224832 b^{25}-1588210119475200 b^{23}+507344899276800 b^{21}-128055803904000 b^{19}+25227583488000 b^{17}-3812168171520 b^{15}+431333683200 b^{13}-35340364800 b^{11}+1999712000 b^9-72864000 b^7+1530144 b^5-15180 b^3+45 b$$
這個式子竟然比$P_{45}$還要復雜得多，但次數倒確實是45次。
仔細觀察便能發現這個多項式的各項系數恰是$P_{45}$系數的$2^n$倍：
$$
\begin{aligned}
45&=45\times2^0\\
15180&=3795\times2^2\\
1530144&=95634\times2^4\\
72864000&=1138500\times2^6\\
\cdots&\cdots\\
3380998255411200&=12300\times2^{38}\\
1039038488248320&=945\times2^{40}\\
197912092999680&=45\times2^{42}\\
17592186044416&=1\times2^{44}
\end{aligned}
$$
設$\sin\theta$展開式的$i$次項系數為$\alpha_i$，$P_{45}$的$i$次項系數為$\beta_i$，則：
$$\alpha_i=\beta_i\cdot2^{i-1}$$
於是容易得到，當$x=2\sin\theta$時：
$$2\sin45\theta=P_{45}(x)$$
於是要解的方程就轉化為：$2\sin45\theta=K$

化簡常數項

多項式可以化簡，這麼復雜的常數項一定也可以化簡。由於左邊是$2\sin45\theta$，可以推測右邊也是$2\sin\varphi$形式的。那麼
$$\frac{1}{2}K=\frac{1}{2}\sqrt{\frac{7}{4}-\sqrt{\frac{5}{16}}-\sqrt{\frac{15}{8}-\sqrt{\frac{45}{64}}}}=\frac{1}{4}\sqrt{7-\sqrt{5}-\sqrt{30-6\sqrt{5}}}$$
是什麼角度的正弦值呢？
注意到(五倍角公式)：
$$16\left(\frac{1}{2}K\right)^5-20\left(\frac{1}{2}K\right)^3+5\left(\frac{1}{2}K\right)=\frac{\sqrt{3}}{2}=\sin\frac{\pi}{3}$$
所以：
$$\frac{1}{2}K=\sin\frac{\pi}{15}$$
怎麼注意到呢？好吧其實是直接用軟件計算$\arcsin K/2$得到12°，再反過來用五倍角公式的。

我在網上找到的所有資料都是計算$\sin12°$，得到其值恰為$K/2$的，似乎沒有直接用$K/2$得到12°的方法。說到底這個純粹是van Roomen為了提高問題難度挖的坑，當時只有對三角函數運用熟練、經驗極其豐富的數學家才能夠得出結果。

解決問題

兩邊都化簡後，問題就簡單了。
$$2\sin45\theta=2\sin\frac{\pi}{15}$$
解得$45\theta=\pi/15+2k\pi$，或$45\theta=14\pi/15+2k\pi$，將將所有滿足條件的$\theta$求出，即可得到所有根$x=2\sin\theta$，具體計算就不干了，這種事情還是交給計算機吧。

其實到這裡只是使用了多項式關於引入的新變量$\theta$的關系式，而沒有得出真正的原函數。通過上面求$x$的過程，很容易得出函數：
$$f(x)=2\sin\left(45\arcsin\left(\frac{x}{2}\right)\right)$$
畫出圖像：

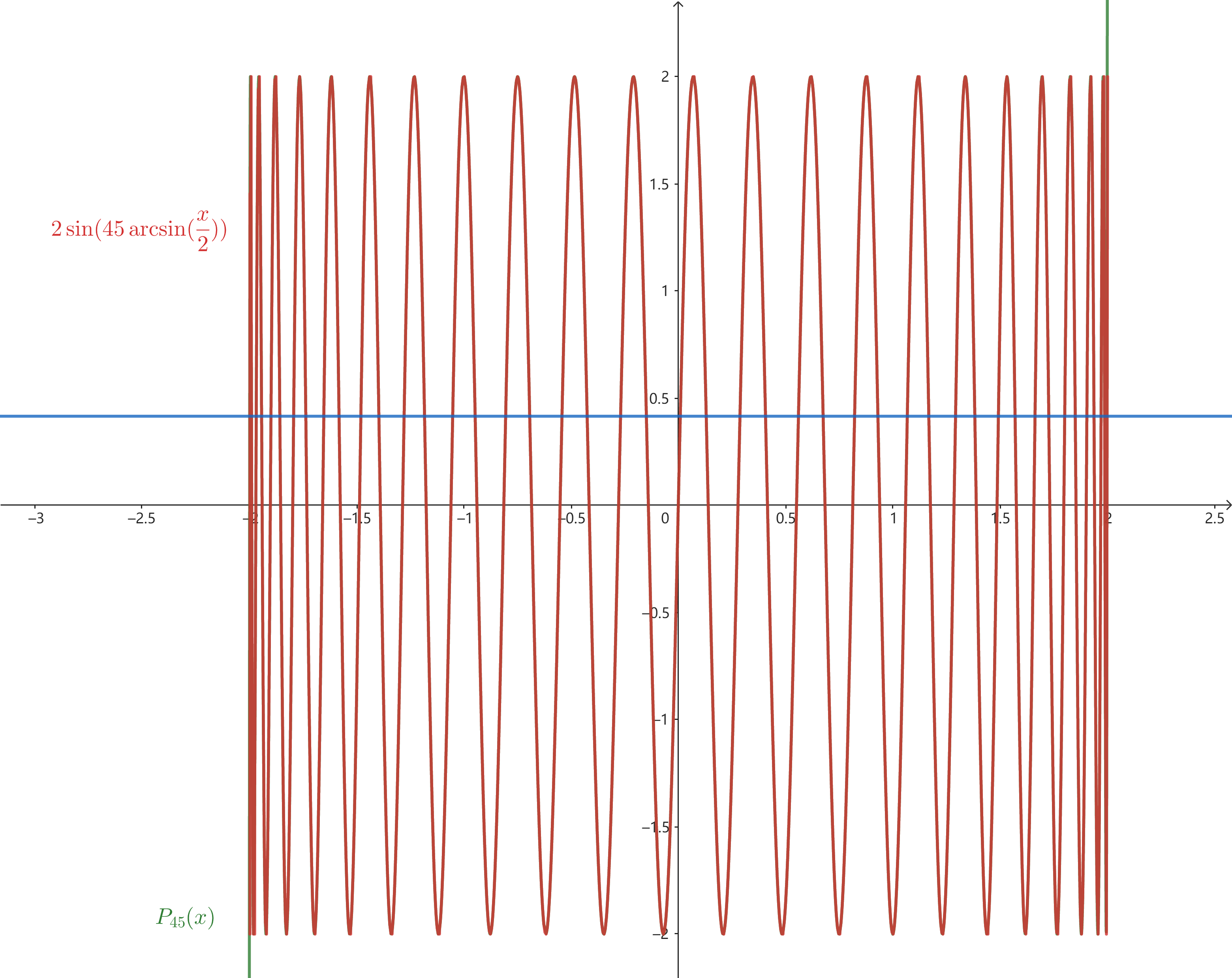
完美！可以看到函數$f(x)$和$P_{45}$在區間$[-2,2]$是完全重合的。但是$P_{45}$對於$f(x)$不僅是展開式，還是一種解析延拓，在此方程中常數項恰在區間$[-2,2]$之間，否則無法用此方法得到解。

4. 其他方法

復數方法

上面我用倍角公式的方法得到了$P_{45}$的化簡，本質上還是誤打誤撞。事實上，若知道原三角函數，還有一種更直接的使用復數和二項式定理的方法求其展開式，下簡述之^[2]。

令$t=\arcsin(x/2)$，那麼：
$$
\begin{aligned}
\sin\left(45\arcsin\left(\frac{x}{2}\right)\right)&=\sin45t\\
&=\mathrm{Im}(e^{45\mathrm{i}t})=\mathrm{Im}((e^{\mathrm{i}t})^{45})\\
&=\mathrm{Im}((\cos t+\mathrm{i}\sin t)^{45})\\
&=\mathrm{Im}\left(\sum_{k=0}^{45}\binom{45}{k}(\mathrm{i}\sin t)^k\cos^{45-k}t\right)\\
&=\frac{1}{\mathrm{i}}\left(\sum_{k=0}^{22}\binom{45}{2k+1}(\mathrm{i}\sin t)^{2k+1}\cos^{45-2k}t)\right)\\
&=\sum_{k=0}^{22}\binom{45}{2k+1}(-1)^k\sin^{2k+1}t(1-\sin^2t)^{22-k})\\
&=\sum_{k=0}^{22}\binom{45}{2k+1}(-1)^k\sin^{2k+1}t\sum_{j=0}^{22-k}\binom{22-k}{j}(-1)^j\sin^{2j}t\\
&=\sum_{k=0}^{22}\sum_{j=0}^{22-k}\binom{45}{2k+1}\binom{22-k}{j}(-1)^{k+j}\sin^{2k+2j+1}t\\
&=\sum_{k=0}^{22}\sum_{j=k}^{22}\binom{45}{2k+1}\binom{22-k}{j-k}(-1)^{j}\sin^{2j+1}t\\
&=\sum_{j=0}^{22}\sum_{k=0}^{j}\binom{45}{2k+1}\binom{22-k}{j-k}(-1)^{j}\sin^{2j+1}t\\
&=\sum_{j=0}^{22}(-1)^j\left[\sum_{k=0}^{j}\binom{45}{2k+1}\binom{22-k}{j-k}\right]\sin^{2j+1}t
\end{aligned}
$$
所以：
$$
\begin{aligned}
f(x)&=2\sin(45\arcsin(\frac{x}{2}))\\
&=\sum_{j=0}^{22}(\frac{-1}{4})^j\left[\sum_{k=0}^{j}\binom{45}{2k+1}\binom{22-k}{j-k}\right]x^{2j+1}\\
&=P_{45}(x)
\end{aligned}
$$
此方法適用於計算更多類似三角函數的展開式。

遞推方法

此外，還有一個相當精彩的方法，通過遞推得到了$P_{45}$與三角函數的關系^[4]。

定義多項式$P_n$：
$$P_n(x)=\sum_{i=0}^{\lfloor n/2\rfloor}(-1)^i\frac{n}{n-i}\binom{n-i}{i}x^{n-2i}$$
容易知道，原方程左端的多項式恰是這樣定義的$P_{45}$。

首先，可以求出$P_n$的遞推公式：
$$P_n(x)=xP_{n-1}(x)-P_{n-2}(x)$$
證明如下：
對於最簡單的情況，因為：
$$
\begin{aligned}
P_1(x)&=x\\
P_2(x)&=x^2-2\\
P_3(x)&=x^3-3x
\end{aligned}
$$
所以：
$$xP_2(x)-P_1(x)=x(x^2-2)-x=x^3-3x=P_3(x)$$
對於整數$n>3$：
$$
\begin{aligned}
xP_{n-1}(x)&=\sum_{i=0}^{\lfloor(n-1)/2\rfloor}(-1)^i\frac{n-1}{n-1-i}\binom{n-1-i}{i}x^{n-2i}\\
&=x^n+\sum_{i=1}^{\lfloor(n-1)/2\rfloor}(-1)^i\frac{n-1}{n-1-i}\binom{n-1-i}{i}x^{n-2i}\\
P_{n-2}(x)&=\sum_{i=0}^{\lfloor n/2-1\rfloor}(-1)^i\frac{n-2}{n-2-i}\binom{n-2-i}{i}x^{n-2-2i}\\
&=\sum_{i=1}^{\lfloor n/2\rfloor}(-1)^{i-1}\frac{n-2}{n-2-(i-1)}\binom{n-2-(i-1)}{i-1}x^{n-2-2(i-1)}\\
&=\sum_{i=1}^{\lfloor n/2\rfloor}(-1)^{i-1}\frac{n-2}{n-1-i}\binom{n-1-i}{i-1}x^{n-2i}
\end{aligned}
$$
接下來根據奇偶性分類討論。
若$2\nmid n$，則$\lfloor n/2\rfloor=\lfloor(n-1)/2\rfloor=(n-1)/2$，
$$xP_{n-1}(x)-P_{n-2}(x)=x^n+\sum_{i=1}^{\lfloor n/2\rfloor}(-1)^i\left[\frac{n-1}{n-1-i}\binom{n-1-i}{i}+\frac{n-2}{n-1-i}\binom{n-1-i}{i-1}\right]x^{n-2i}$$
注意中間部分：
$$
\begin{aligned}
&\frac{n-1}{n-1-i}\binom{n-1-i}{i}+\frac{n-2}{n-1-i}\binom{n-1-i}{i-1}\\
=&\frac{n-1}{n-1-i}\cdot\frac{(n-1-i)!}{i!(n-1-2i)!}+\frac{n-2}{n-1-i}\cdot\frac{(n-1-i)!}{(i-1)!(n-2i)!}\\
=&\frac{(n-i)!}{(n-i)i!(n-2i)!}\cdot[\frac{(n-1)(n-2i)}{n-1-i}+\frac{i(n-2)}{n-1-i}]\\
=&\frac{n}{n-i}\cdot\frac{(n-i)!}{i!(n-2i)!}\\
=&\frac{n}{n-i}\binom{n-i}{i}
\end{aligned}
$$
代回原式：
$$
\begin{aligned}
xP_{n-1}(x)-P_{n-2}(x)&=x^n+\sum_{i=1}^{\lfloor n/2\rfloor}(-1)^i\frac{n}{n-i}\binom{n-i}{i}x^{n-2i}\\
&=\sum_{i=0}^{\lfloor n/2\rfloor}(-1)^i\frac{n}{n-i}\binom{n-i}{i}x^{n-2i}\\
&=P_n(x)
\end{aligned}
$$
若$2\mid n$，則$\lfloor n/2\rfloor=\lfloor(n-1)/2\rfloor+1=n/2$，
$$
\begin{aligned}
xP_{n-1}(x)-P_{n-2}(x)=&\sum_{i=0}^{\lfloor n/2\rfloor-1}(-1)^i\frac{n}{n-i}\binom{n-i}{i}x^{n-2i}-(-1)^{n/2-1}\frac{n-2}{n/2-1}\binom{n/2-1}{n/2-1}\\
=&\sum_{i=0}^{\lfloor n/2\rfloor-1}(-1)^i\frac{n}{n-i}\binom{n-i}{i}x^{n-2i}+2(-1)^{n/2}
\end{aligned}
$$
當$i=\lfloor n/2\rfloor=n/2$時，
$$(-1)^i\frac{n}{n-i}\binom{n-i}{i}x^{n-2i}=(-1)^{n/2}\frac{n}{n/2}\binom{n/2}{n/2}x^0=2(-1)^{n/2}$$
所以：
$$xP_{n-1}(x)-P_{n-2}(x)=\sum_{i=0}^{\lfloor n/2\rfloor}(-1)^i\frac{n}{n-i}\binom{n-i}{i}x^{n-2i}=P_n(x)$$

然後來看三角函數中的遞推關系。
先從一個最基本的關系開始，即喜聞樂見的積化和差：
$$\cos A\cos B=\frac{\cos(A+B)+\cos(A-B)}{2}$$
整理一下可得：
$$2\cos(A+B)=4\cos A\cos B-2\cos(A-B)$$
令$A=(n-1)\alpha$，$B=\alpha$，則可以得到：
$$2\cos n\alpha=2\cos\alpha\cdot2\cos(n-1)\alpha-2\cos\alpha$$
這時很容易看出此遞推關系與$P_n$的相似性，若令$x=2\cos\alpha$，則：
$$
\begin{aligned}
P_1(x)&=x=2\cos\alpha\\
P_2(x)&=x^2-2=4\cos^2\alpha-2=2\cos2\alpha\\
P_3(x)&=x^3-3x=8\cos^3\alpha-6\cos\alpha=2\cos3\alpha
\end{aligned}
$$
對於$n>3$，由於遞推關系一致，可以得到如下等式：
$$P_n(2\cos\alpha)=2\cos n\alpha$$
正弦函數的關系式可以用余弦函數的關系式推出。
令$\alpha=\beta-\pi/2$代入上式：
$$
\begin{aligned}
P_n\left(2\cos\left(\beta-\frac{\pi}{2}\right)\right)=&2\cos n\left(\beta-\frac{\pi}{2}\right)\\
P_n(2\sin\beta)=&2\cos\left(n\beta-\frac{n\pi}{2}\right)
\end{aligned}
$$
若$2\nmid n$，則可化為更規整的形式：
$$P_n(2\sin\beta)=2\sin n\beta\cdot(-1)^{\frac{n-1}{2}},\quad2\nmid n$$

事實上，上面的三角函數遞推過程就是$n$倍角公式的遞推計算過程，這種方法就是將最初的三角函數方法規范化，形成一種確定的技巧。
由這樣的推導可知，使用余弦函數也可化簡多項式，原函數為$2\cos(45\arccos(x/2))$，而且余弦函數對於此類多項式的使用范圍更廣，最初使用正弦函數成功化簡確實是誤打誤撞，要不是恰好45滿足$2\nmid n$，$2\mid(n-1)/2$，就得不到答案了。(運氣真好~)

5. 切比雪夫多項式

在上述遞歸方法中定義的$P_n$，與第一類切比雪夫多項式很類似，這個多項式通常用$T_n$表示，定義為：
$$
\begin{aligned}
T_0(x)&=1\\
T_1(x)&=x\\
T_n(x)&=2xT_{n-1}(x)-T_{n-2}(x)
\end{aligned}
$$
區別在於遞推公式系數中的2，這就導致了兩類多項式對應三角函數的區別：
$$
\begin{aligned}
&T_n(x)=\cos(n\arccos(x)),\quad x\in[-1,1]\\
&P_n(x)=2\cos\left(n\arccos\left(\frac{x}{2}\right)\right),\quad x\in[-2,2]\\
&T_n(\cos\theta)=\cos n\theta\\
&P_n(2\cos\theta)=2\cos n\theta
\end{aligned}
$$
切比雪夫多項式於1854年由切比雪夫(Chebyshev)引入，之後在逼近理論中被廣泛使用。而究其歷史，則早在正式提出的250年前就已被發現與使用，Viète等數學家的洞察力與遠見實在令人驚嘆。

6. 參考

[1]Adriaan van Roomen. Ideae mathematicae pars prima, sive methodus polygonorum, 1593.
[2]R. L. Herman. van Roomen’s Problem, 2021
http://people.uncw.edu/hermanr/mat346/van_Roomen_s_Problem.pdf
[3]參考文獻使用符號$\sin^{-1}$，本文為避免歧義，統一使用符號$\arcsin$
[4]Van Roomen’s Problem: Solution Explained
http://fermatslasttheorem.blogspot.com/2007/02/van-roomens-problem-solution-explained.html