从欧拉公式到巴塞尔问题

欧拉公式

《微积分入门》使用欧拉公式严格地定义了三角函数，这里只参考原书推导欧拉公式，不重新定义三角函数。

定义复数$e=\cos(\theta)+\mathrm{i}\sin(\theta)$，$\vert e\vert^2=\cos^2(\theta)+\sin^2(\theta)=1$。这个复数$e$并不是实际的数，而是表示一种变换，用这个复数来表示复平面的旋转：
$$R_e: z\to z’=e\cdot z$$
需要确定的就是复数$e$关于角$\theta$的非三角函数形式的函数$e(\theta)$。
首先，旋转两次的复合可以用$e$的乘积表示，而对于旋转的角，则是相加，由此可得：
$$e(\theta+\varphi)=e(\theta)\cdot e(\varphi)\quad(1)$$
令$\varphi=0$，可得$e(\theta+0)=e(\theta)\cdot e(0)$，于是得到：
$$e(0)=1$$
令$\varphi=-\theta$，可得$e(0)=e(\theta)\cdot e(-\theta)$，于是得到：
$$e(-\theta)=\frac{1}{e(\theta)}=\overline{e(\theta)}$$
同时很容易得到：对于正整数$n$，$e(n\theta)=e(\theta)^n$，所以：
$$e(\theta)=e(\frac{\theta}{n})^n$$
当$n\to\infty$时，$\theta/n\to0$，$e(\theta/n)\to1$，令：
$$e(\frac{\theta}{n})=1+\sigma_n,\quad\sigma_n\to0$$
则：
$$e(\theta)=(1+\sigma_n)^n$$
此时，观察$1\cdot e(\theta/n)=e(\theta/n)$：

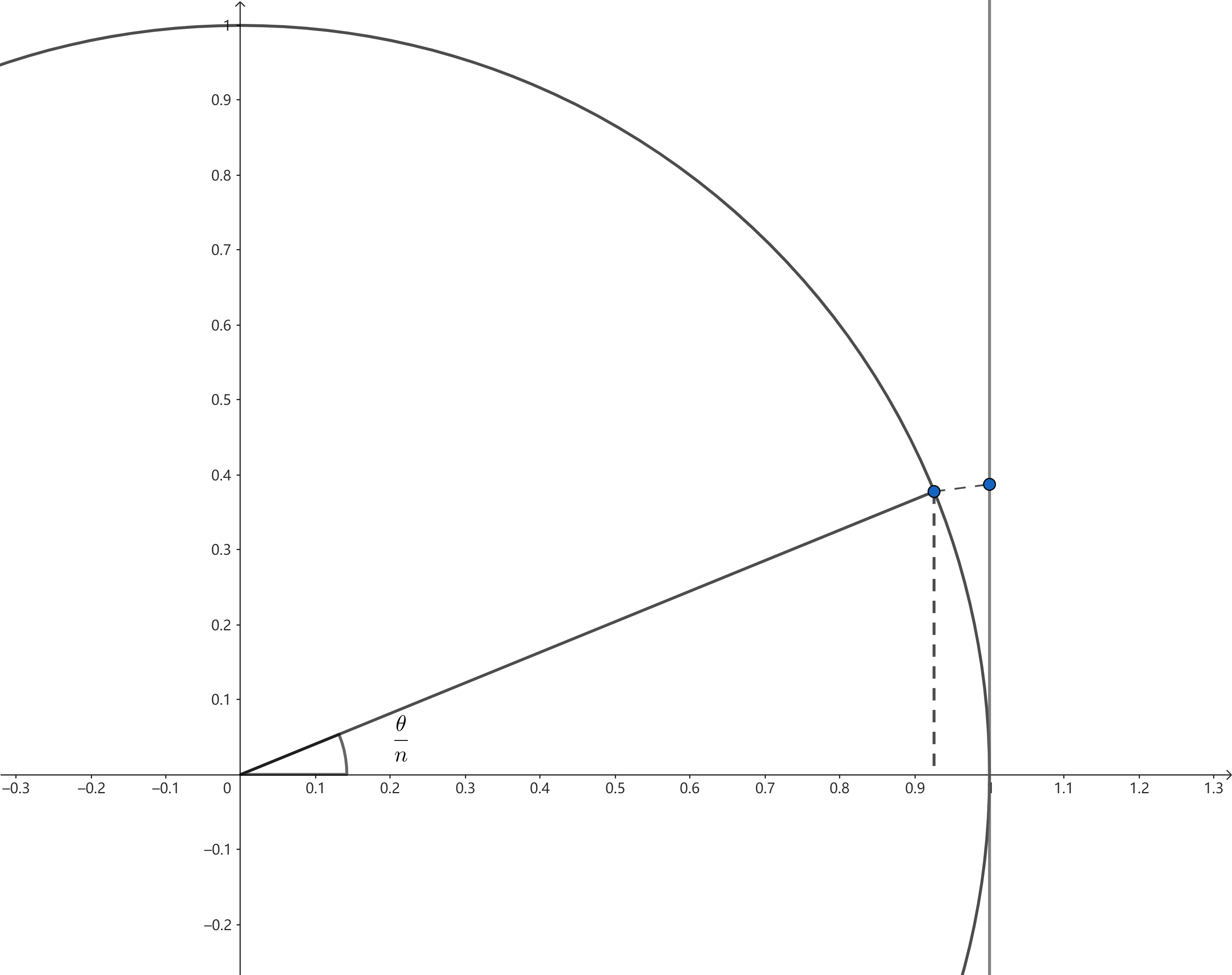
可以看到，$e(\theta/n)$很接近$1+(\theta/n)\mathrm{i}$，于是设：
$$\sigma_n=\frac{1}{n}(\tau_n+\theta\mathrm{i}),\quad\tau_n\to0$$
(加上一个很小的$\tau$是为了严格性)
于是得到：
$$e(\theta)=(1+\frac{\theta\mathrm{i}}{n}+\frac{\tau}{n})^n=(1+\frac{\theta\mathrm{i}}{n})^n(1+\frac{z_n}{n})^n$$
其中：
$$z_n=\frac{\tau_n}{1+\theta\mathrm{i}/n}\to0$$

引理1：对于复数列$\{z_n\}$，若$\lim_{n\to\infty}z_n=0$，那么$\lim_{n\to\infty}(1+z_n/n)^n=1$。具体证明不再赘述，见《微积分入门》。

由此引理可得：
$$e(\theta)=\lim_{n\to\infty}(1+\frac{\theta\mathrm{i}}{n})^n$$
可以证明此函数是绝对值为1的连续复值函数，且满足条件(1)，具体见《微积分入门》。
又由$e^z=\lim_{n\to\infty}(1+z/n)^n$，可得：
$$e(\theta)=\lim_{n\to\infty}(1+\frac{\theta\mathrm{i}}{n})^n=e^{\mathrm{i}\theta}=\cos(\theta)+\mathrm{i}\sin(\theta)$$
这就是欧拉公式。

因为$\lim_{n\to\infty}(1+z/n)^n=\sum_{n=0}^{\infty}z^n/n!$，所以：
$$e(\theta)=1+\sum_{n=1}^{\infty}\frac{(\mathrm{i}\theta)^n}{n!}=1+\frac{\mathrm{i}\theta}{1!}-\frac{\theta^2}{2!}-\frac{\mathrm{i}\theta^3}{3!}+\frac{\theta^4}{4!}+\cdots$$
很容易得到正余弦函数的泰勒展开：
$$
\begin{cases}
\cos(\theta)=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\cdots\\
\sin(\theta)=\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots
\end{cases}
$$

正弦函数因式分解

因为$\sin(\pi)=0$，所以可以将正弦函数因式分解为：
$$\sin(x)=ax(x+\pi)(x-\pi)(x+2\pi)(x-2\pi)\cdots$$
注意到极限：
$$\lim_{x\to0}\frac{\sin(x)}{x}=1$$
于是将上式两边除以$x$并取极限：
$$1=a\pi(-\pi)(2\pi)(-2\pi)\cdots$$
所以：
$$a=\frac{1}{\pi(-\pi)(2\pi)(-2\pi)\cdots}$$
代回原式：
$$\sin(x)=x(1+\frac{x}{\pi})(1-\frac{x}{\pi})(1+\frac{x}{2\pi})(1-\frac{x}{2\pi})\cdots$$

巴塞尔问题

巴塞尔问题即为求如下级数的值：
$$\sum_{n=1}^{\infty}\frac{1}{n^2}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots$$
这个问题有很多解法，这里写一种使用正弦函数的解法。

现在，有两个正弦函数的表达式：
$$
\begin{aligned}
\sin(x)=&x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots\\
\sin(x)=&x(1+\frac{x}{\pi})(1-\frac{x}{\pi})(1+\frac{x}{2\pi})(1-\frac{x}{2\pi})\cdots
\end{aligned}
$$
将下式展开：
$$
\begin{aligned}
\sin(x)&=x(1+\frac{x}{\pi})(1-\frac{x}{\pi})(1+\frac{x}{2\pi})(1-\frac{x}{2\pi})\cdots\\
&=x(1-\frac{x^2}{\pi^2})(1-\frac{x^2}{4\pi^2})(1-\frac{x^2}{9\pi^2})\cdots\\
&=[x-(\frac{x^3}{\pi^2}+\frac{x^3}{4\pi^2}+\frac{x^3}{9\pi^2})+(\frac{x^5}{4\pi^4}+\frac{x^5}{9\pi^4}+\frac{x^5}{36\pi^4})-\frac{x^7}{36\pi^6}](1-\frac{x^2}{16\pi^2})\cdots\\
&=x-\sum_{n=1}^{\infty}\frac{x^3}{n^2\pi}+ax^5-bx^7+\cdots
\end{aligned}
$$
比较$x$的次数可得到等式：
$$-\frac{x^3}{3!}=-\frac{x^3}{6}=-\sum_{n=1}^{\infty}\frac{x^3}{n^2\pi}$$
于是得到：
$$\sum_{n=1}^{\infty}\frac{1}{n^2}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots=\frac{\pi^2}{6}$$