多個圓的最小外切三角形-2

1. 回顧

還是繼續對等大情況的研究。
算了一下上一篇所說的兩個數列，並分別計算比較了對應的面積，於是記錄一下研究進展。
為方便起見，接下來直接稱三角形數個圓的外切等邊三角形為全三角形，半三角形數個圓的外切直角三角形為半三角形(雖然這個定義很奇怪，名稱更奇怪，但是Who cares？)。三角形數和半三角形數分別用$a_k,b_n$表示，圓的個數用$c$表示。

現在有兩個數列：

1. 三角形數：
   $$a_k=k(k+1)/2$$
2. 半三角形數：
   $$
   b_n=\begin{cases}
   n^2/4,\quad 2\mid n\\
   (n^2-1)/4,\quad 2\nmid n
   \end{cases}
   $$

在上一篇中以提出猜想：當圓的數目恰為三角形數時，最小外切三角形即為圓按照平面六角密堆積式排列之外切等邊三角形(全三角形)；當圓的數目恰為半三角形數時，最小外切三角形即為圓按照類似方法排列之外切直角三角形(半三角形)。如圖所示：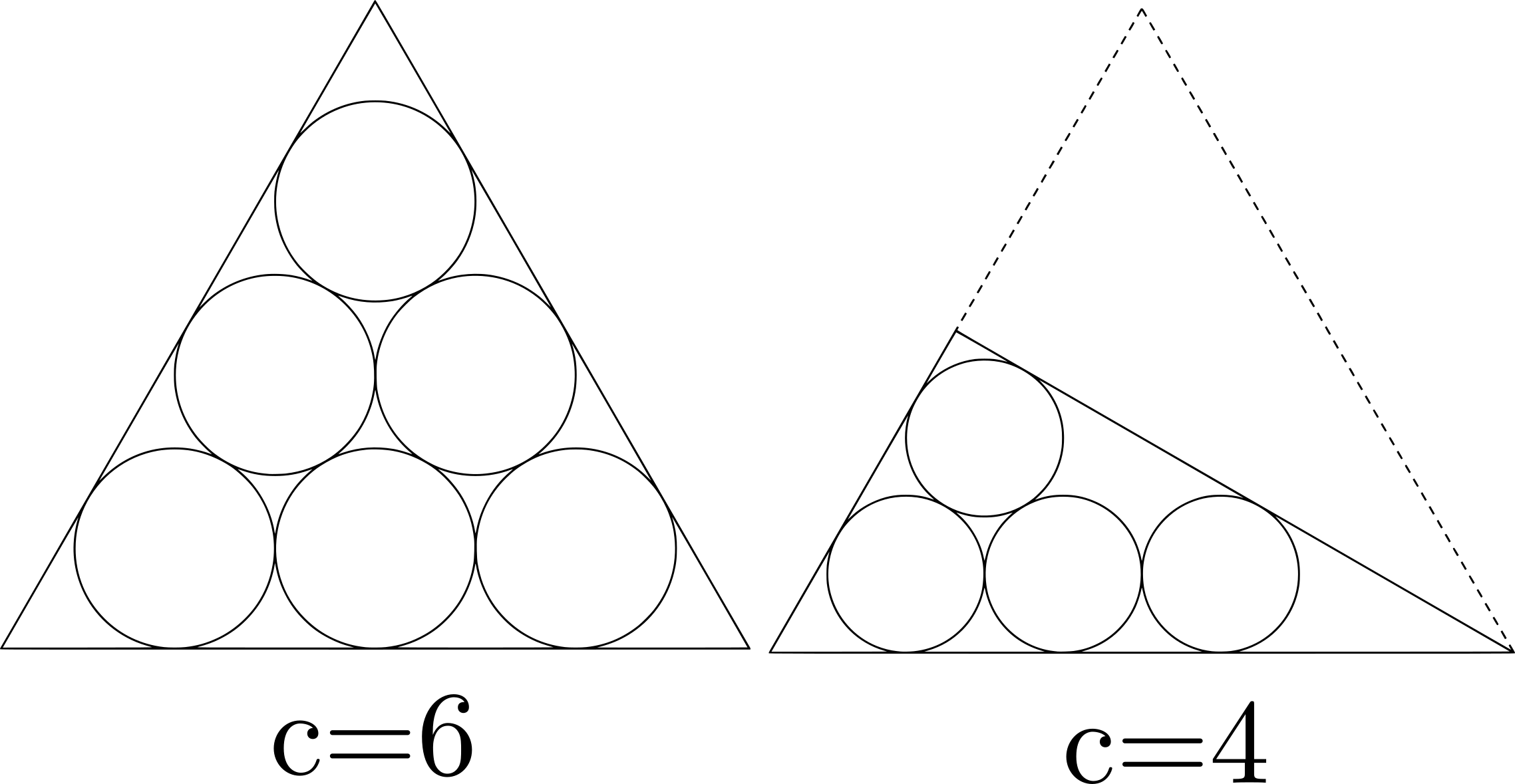

同時，這兩種形式的三角形面積可以用$n$和$k$表示：
當$c=a_k$時，
$$S_k=\sqrt{3}k^2+(6-2\sqrt{3})k+4\sqrt{3}-6$$
當$c=b_n$時，
$$S_n=\frac{\sqrt{3}}{2}n^2+(3-\sqrt{3})n+2\sqrt{3}-3$$
此時問題轉化成了對這兩個數列的研究(似乎已經不是幾何問題了)。

2. 對數列的探究

粗略觀察兩組數列，會發現$k=n$時，$a_k\approx2b_n$，$S_k=2S_n$；兩組數值分布不均，但基本在兩個三角形數之間存在1至2個半三角形數，同時存在$a_k=b_n$的情況；當$c=b_n=a_k$時，$S_k<S_n$，當$c=b_n<a_k$時，$S_k>S_n$或$S_k<S_n$均有可能。

作出數據圖如下，橫軸數據為恰是三角形數或半三角形數的圓個數(從4開始)，縱軸為相應的全三角形或半三角形面積，黑色表示全三角形，紅色表示半三角形：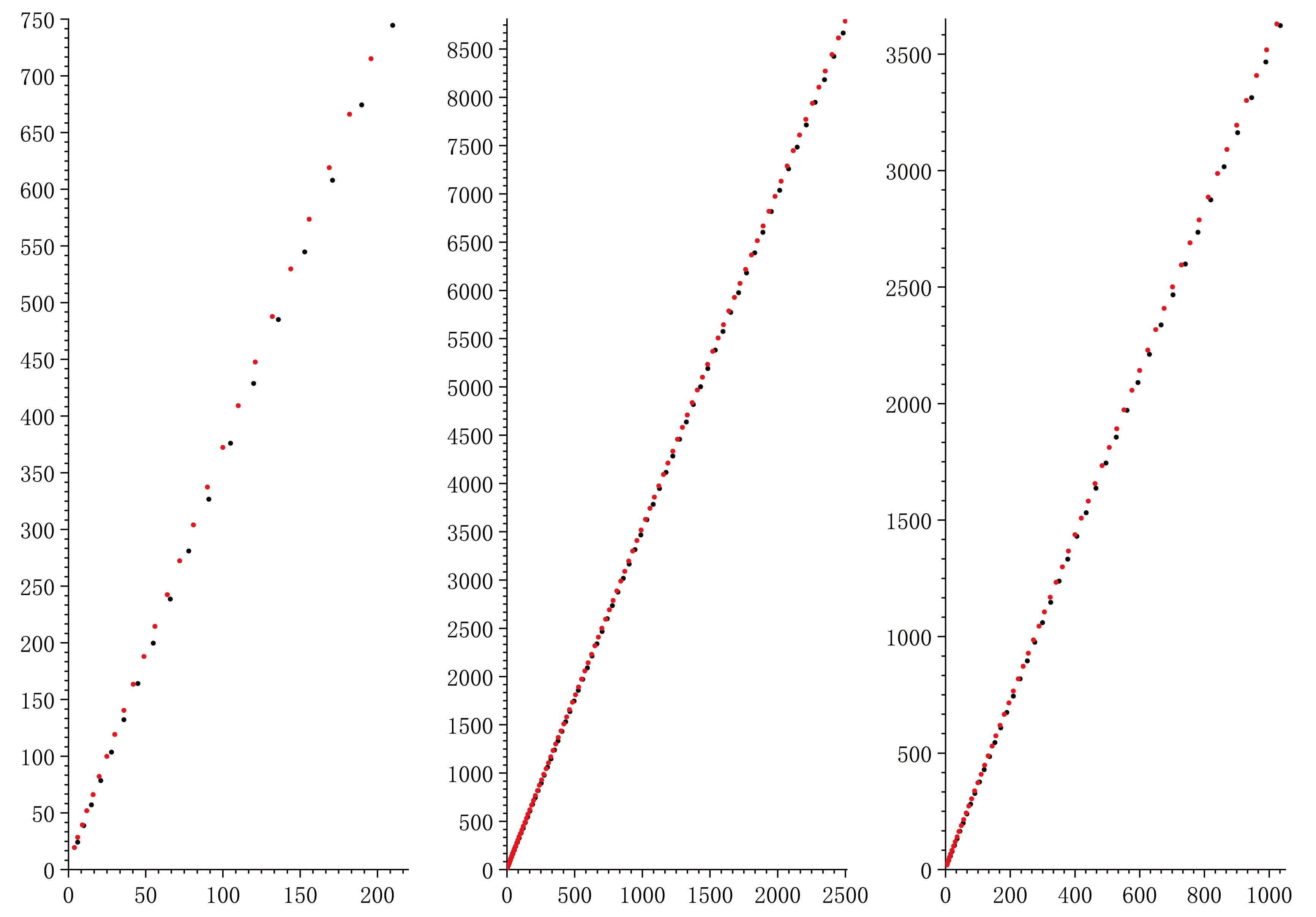

可以看到，面積與圓的數量大致呈正比關系，上述的幾個觀察結果在圖上也反映得很清晰。

首先可以求出數列的遞推式：
$$a_{k+1}=a_k+k+1$$
$$
b_{n+1}=\begin{cases}
b_n+n/2,\quad 2\mid n\\
b_n+(n+1)/2,\quad 2\nmid n
\end{cases}
$$
這兩個數列的遞推都很有意思，$a$是從0開始加上連續自然數(實際數列從1開始)，$b$也是從0開始加連續自然數，但每個自然數加兩次。

相等的情況

要研究兩個數列數值的大小關系，可以從某一個相等的值開始考慮。
設$a_k=b_n$，則可以得到$n$與$k$的關系：$① n=\sqrt{2k^2+2k}$或$②n=\sqrt{2k^2+2k+1}$，這兩個式子包含了$n$的奇偶性信息，由於$k$是整數，①式得到的$n$必然是偶數，②式得到的$n$必然是奇數。但是兩式中$k$的奇偶性沒有限制，前4組$n$與$k$為：
$$
\begin{align*}
5&=\sqrt{2\times3^2+2\times3+1}\\
12&=\sqrt{2\times8^2+2\times8}\\
29&=\sqrt{2\times20^2+2\times20+1}\\
70&=\sqrt{2\times49^2+2\times49}
\end{align*}
$$
整體觀察數據，發現
$$
\begin{align*}
2\nmid n,\quad2\nmid k\\
2\mid n,\quad2\mid k\\
2\nmid n,\quad2\mid k\\
2\mid n,\quad2\nmid k
\end{align*}
$$
這4種情況周期性出現。

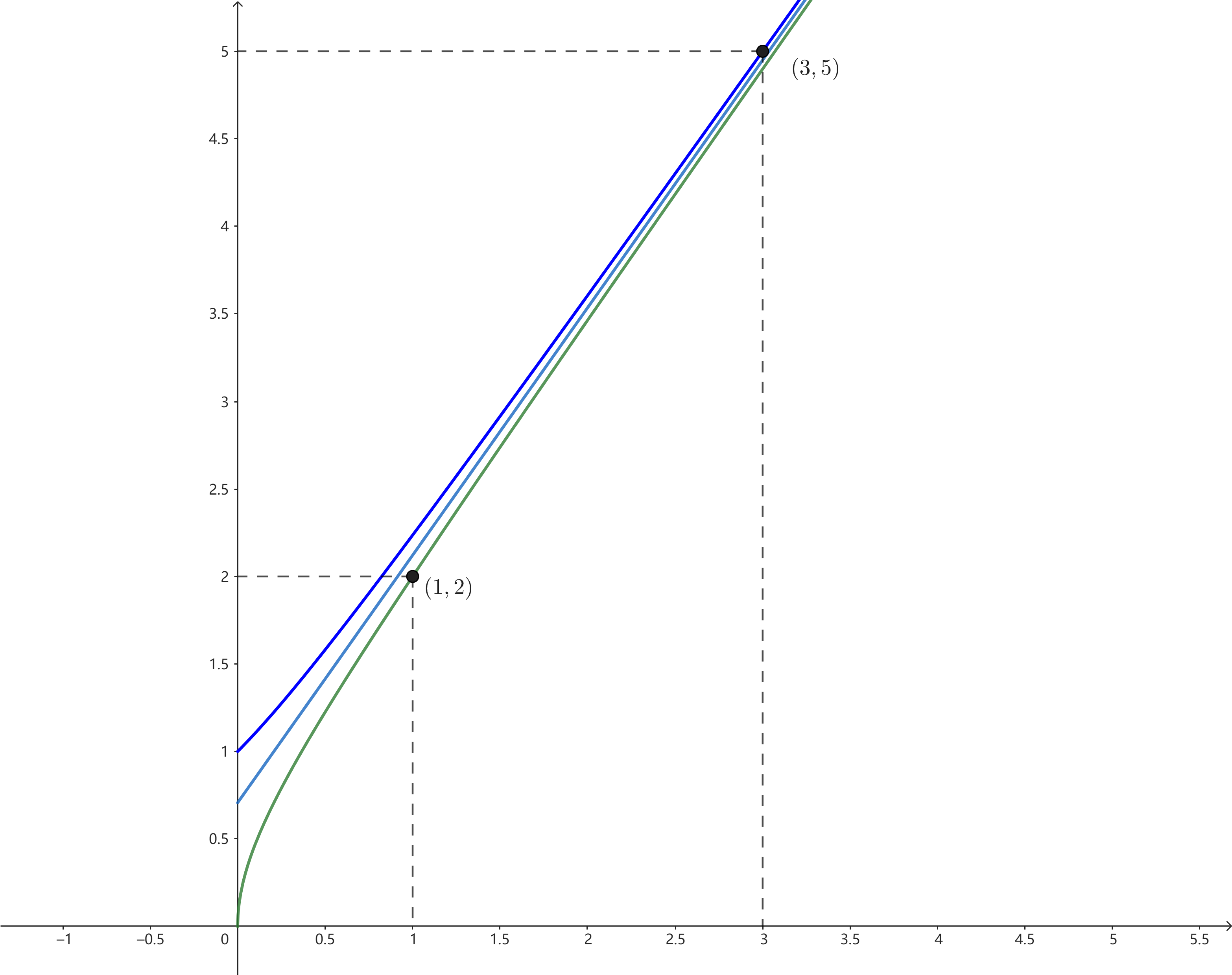如圖，$\sqrt{2x^2+2x}$和$\sqrt{2x^2+2x+1}$是$\sqrt2(x+1/2)$的兩條漸近線，而一組$n$與$k$就表示這兩條漸近線上的一個整點(整點$(1,2)$不算)。這似乎與$\sqrt2$的連分數表示有關系，結論應該可以用相關知識證明，但我對數論了解不多，就不繼續了。 顯然，由於兩條漸近線上的整點是無窮多的，$a_k=b_n$的數量也是無窮的，但出現間隔越來越大。

一些遞推

當$a_k=b_n$時，寫出$n$和$k$關於$a_k$和$b_n$的關系式：
$$k=\sqrt{2a_k+1/4}-1/2$$
$$
n=\begin{cases}
2\sqrt{b_n},\quad 2\mid n\\
2\sqrt{b_n+1/4},\quad 2\nmid n
\end{cases}
$$
代入遞推式：
$$a_{k+1}=a_k+\sqrt{2a_k+1/4}+1/2$$
$$
b_{n+1}=\begin{cases}
b_n+\sqrt{b_n},\quad 2\mid n\\
b_n+\sqrt{b_n+1/4}+1/2,\quad 2\nmid n
\end{cases}
$$
因為$a_k=b_n$，所以$\sqrt{2a_k+1/4}+1/2>\sqrt{b_n}$，$\sqrt{2a_k+1/4}+1/2>\sqrt{b_n+1/4}+1/2$，可知$b_{n+1}<a_{k+1}$。將這個結果再代回遞推式，又可以得到$b_{n+2}<a_{k+2}$。當然，這些都是顯而易見的，比較$b_{n+2}$和$a_{k+1}$的大小則計算稍繁瑣，
$$
b_{n+2}=\begin{cases}
b_n+\sqrt{b_n}+\sqrt{b_n+\sqrt{b_n}+1/4}+1/2,\quad 2\mid n\\
b_n+\sqrt{b_n+1/4}+\sqrt{b_n+\sqrt{b_n+1/4}+1/2}+1/2,\quad 2\nmid n
\end{cases}
$$
因為$a_k=b_n>0$，所以：
$$
\begin{align*}
\sqrt{2a_k+1/4}&<\sqrt{b_n}+\sqrt{b_n+\sqrt{b_n}+1/4}\\
\sqrt{2a_k+1/4}&<\sqrt{b_n+1/4}+\sqrt{b_n+\sqrt{b_n+1/4}+1/2}
\end{align*}
$$
所以$b_{n+2}>a_{k+1}$。
若條件改為$a_k<b_n$，根據上式仍能得到$b_{n+2}>a_{k+1}$，於是可知不存在2個三角形數之間存在3個半三角形數的情況，即2個三角形數之間存在1至2個半三角形數。

之後可繼續代回遞推式計算，比較大小，但計算太復雜，就不算下去了。
直接觀察數據可知，當$k=3$，$n=5$時，
$$
\begin{align*}
a_k=b_n\\
a_k<b_{n+1}<a_{k+1}\\
a_{k+1}<b_{n+2}<a_{k+2}\\
a_{k+2}<b_{n+3}<\textcolor{red}{b_{n+4}}<a_{k+3}\\
\cdots
\end{align*}
$$
對其他滿足$a_k=b_n$的$k$和$n$，結果也大致如此，這樣的規律是否恆成立？何時2個三角形數之間存在2個半三角形數？
比對面積大小，發現當2個三角形數之間存在2個半三角形數時，較小的半三角形數對應面積小於大三角形數對應面積，而較大的半三角形數對應面積大於大三角形數對應面積，是否必然如此？
這些問題留到以後考慮吧。

比較面積

接下來寫出$S_k$和$S_n$與$c$的關系式。
若$c=a_k=k(k+1)/2$，則$k=\sqrt{2a_k+1/4}-1/2$，代入到面積公式中：
$$S_k=2\sqrt3a_k+(6-3\sqrt3)\sqrt{2a_k+1/4}+11\sqrt3/2-9$$
若$c=b_n$，則
$$
n=\begin{cases}
2\sqrt{b_n},\quad 2\mid n\\
2\sqrt{b_n+1/4},\quad 2\nmid n
\end{cases}
$$
代入到面積公式：
$$
S_n=\begin{cases}
2\sqrt3b_n+(6-2\sqrt3)\sqrt{b_n}+2\sqrt3-3,\quad 2\mid n\\
2\sqrt3b_n+(6-2\sqrt3)\sqrt{b_n+1/4}+5\sqrt3/2-3,\quad 2\nmid n
\end{cases}
$$
本來以為這兩條曲線也是某條曲線的漸近線，但其實兩個函數差的極限是$\sqrt{3}/2$，並不是漸近線。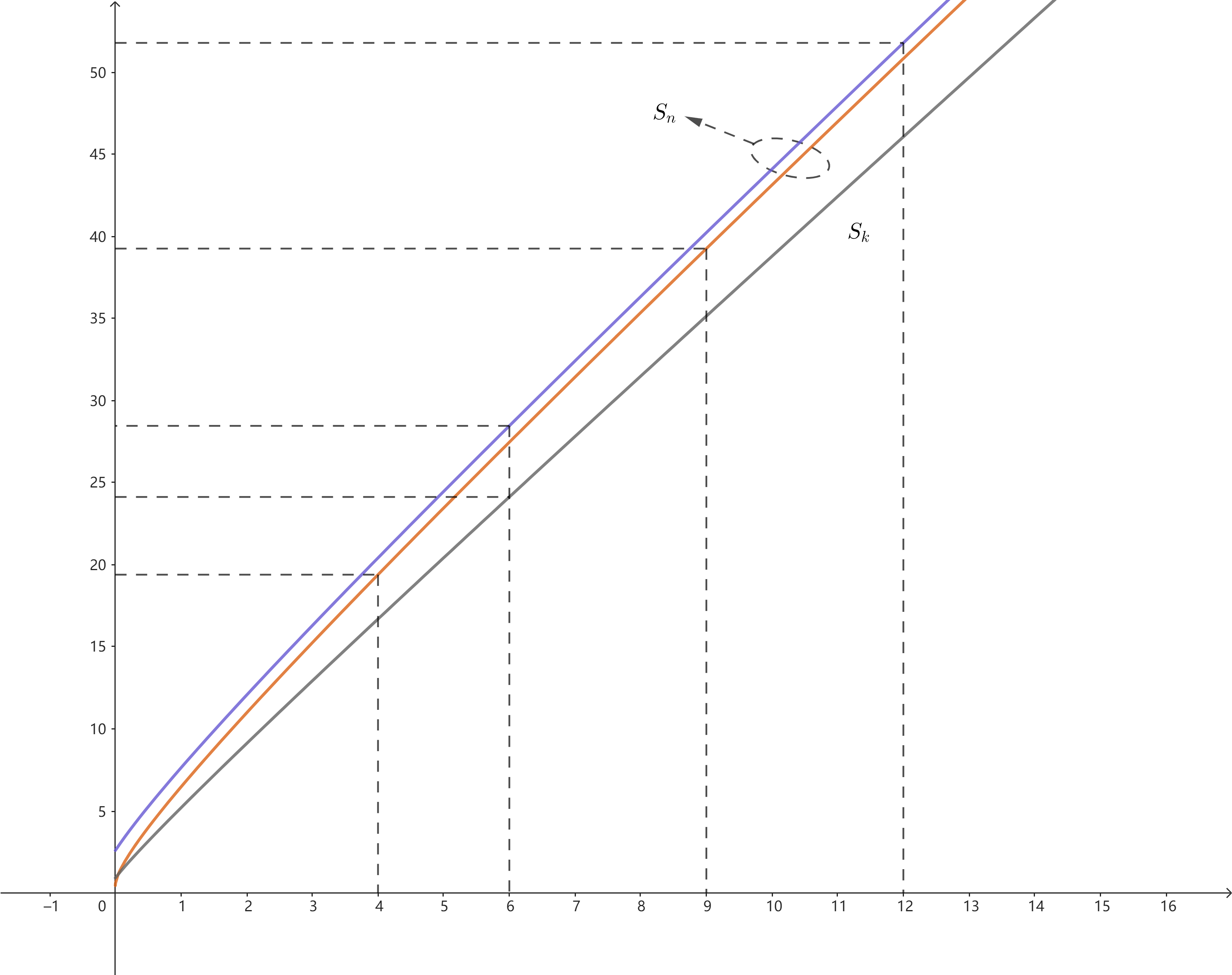

這張圖清晰的反映了面積與圓數量的接近正比的關系($1/2$次項幾乎可忽略)，並且這條曲線斜率很大(注意圖中橫縱坐標比值是$1:4$)。

先看最簡單的情況：$c=a_k=b_n$，設：
$$
f(c)=S_n-S_k=\begin{cases}
(6-2\sqrt3)\sqrt{c}-(6-3\sqrt3)\sqrt{2c+1/4}-7\sqrt3/2+6,\quad 2\mid n\\
(6-2\sqrt3)\sqrt{c+1/4}-(6-3\sqrt3)\sqrt{2c+1/4}-3\sqrt3+6,\quad 2\nmid n
\end{cases}
$$
若$2\mid n$，當$c>0.04348\cdots$時，$f(c)>0$；若$2\nmid n$，$f(c)$恆大於0.
所以當$c=a_k=b_n$，$S_k<S_n$

關鍵問題是$a_{k-1}<c=b_n=a_k-d(d\in\mathbb{N^+})$，而$S_k<S_n$的情況，設：
$$
g(c,d)=S_n-S_k=\begin{cases}
-2\sqrt3d+(6-2\sqrt3)\sqrt{c}-(6-3\sqrt3)\sqrt{2(c+d)+1/4}-7\sqrt3/2+6,\quad 2\mid n\\
-2\sqrt3d+(6-2\sqrt3)\sqrt{c+1/4}-(6-3\sqrt3)\sqrt{2(c+d)+1/4}-3\sqrt3+6,\quad 2\nmid n
\end{cases}
$$
理論上，解$g(c,d)>0$的不等式，可以得到$d$的范圍，但這個方程沒那麼好解，直接解會得到長得離譜的答案。
那就先畫個三維曲面圖吧($2\mid n$)：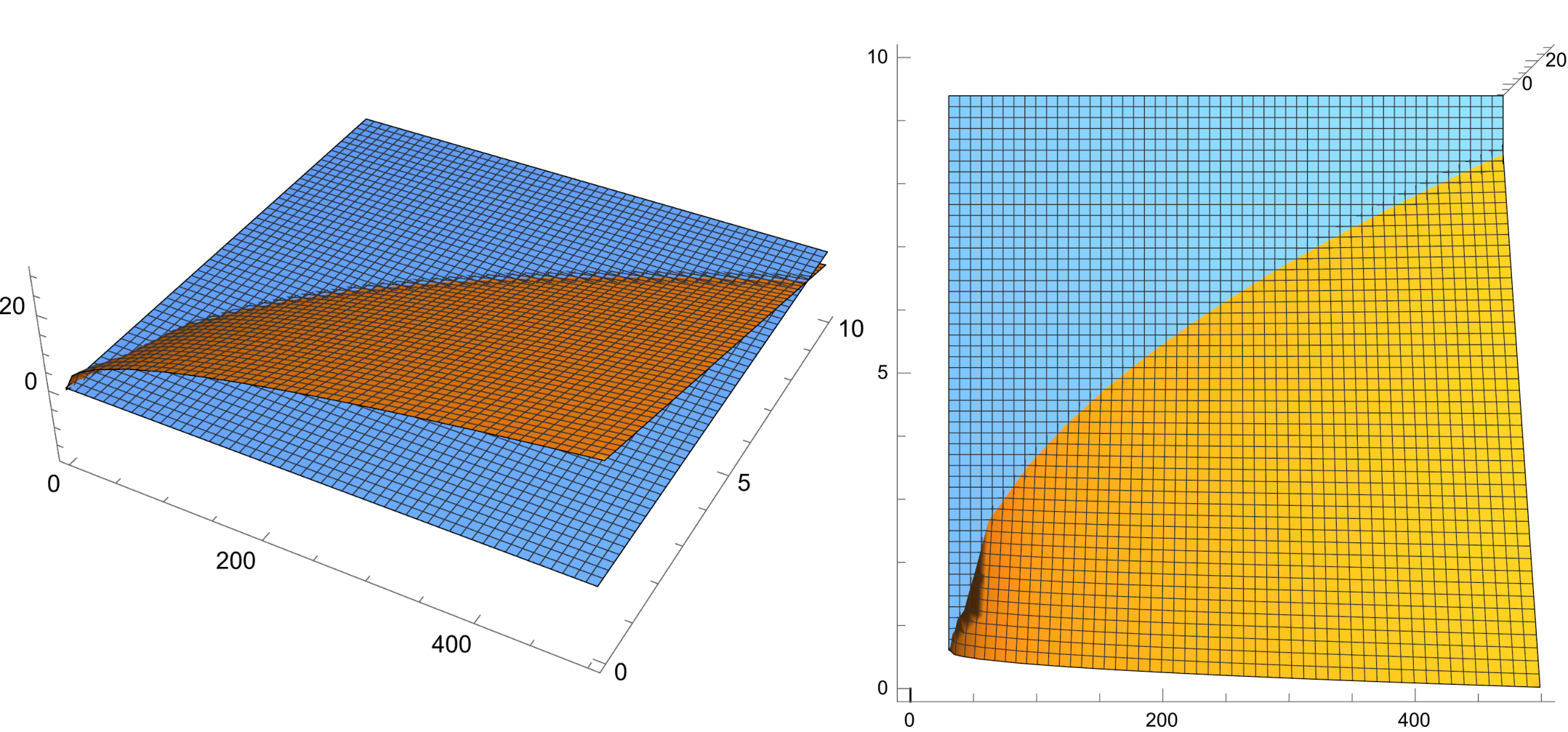

圖中黃色的曲面是
$$g(c,d)=-2\sqrt3d+(6-2\sqrt3)\sqrt{c}-(6-3\sqrt3)\sqrt{2(c+d)+1/4}-7\sqrt3/2+6$$
藍色的曲面是$z=0$，所以黃色曲面在藍色曲面上的部分就表示不等式$g(c,d)>0$成立的部分。那麼要求的就是這兩個曲面的交線，曲線以下即使$d$的范圍(當然，還有滿足$2\mid n$，$c$和$d$取整等條件)。於是直接求解$g(c,d)=0$，神奇的事情發生了，解不等式時的超長答案消失了，取而代之的是兩組非常友善的解：
$$
\begin{align*}
d_1&=-\frac{\sqrt{3}}{2}\cdot\sqrt{\left(14-8 \sqrt{3}\right) c+\left(22 \sqrt{3}-38\right) \sqrt{c}-15 \sqrt{3}+26}+\left(\sqrt{3}-1\right) \sqrt{c}-2 \sqrt{3}+\frac{7}{2}\\
d_2&=\frac{\sqrt{3}}{2}\cdot \sqrt{\left(14-8 \sqrt{3}\right) c+\left(22 \sqrt{3}-38\right) \sqrt{c}-15 \sqrt{3}+26}+\left(\sqrt{3}-1\right) \sqrt{c}-2\sqrt{3}+\frac{7}{2}
\end{align*}
$$
但為什麼會有兩組解？無所謂，直接代回去檢驗就可以了，發現$d_1$是可行的(其實也有誤差，但太小就直接忽略了)。
對$2\nmid n$重復一遍操作，得到(當然，這個其實也是近似的)：
$$d=\sqrt{3c+3/4}-\sqrt{c+1/4}-\frac{\sqrt{2}}{4}\cdot\sqrt{-4 \sqrt{3} (4 c+1)+8 (4 c+1)+52 c-32 \sqrt{3} c+66 \sqrt{3} \sqrt{4 c+1}-114 \sqrt{4 c+1}-98 \sqrt{3}+169}-2\sqrt{3}+\frac{15}{4}$$
這之後還得向下取整，最後得到$1000$以下取整圖：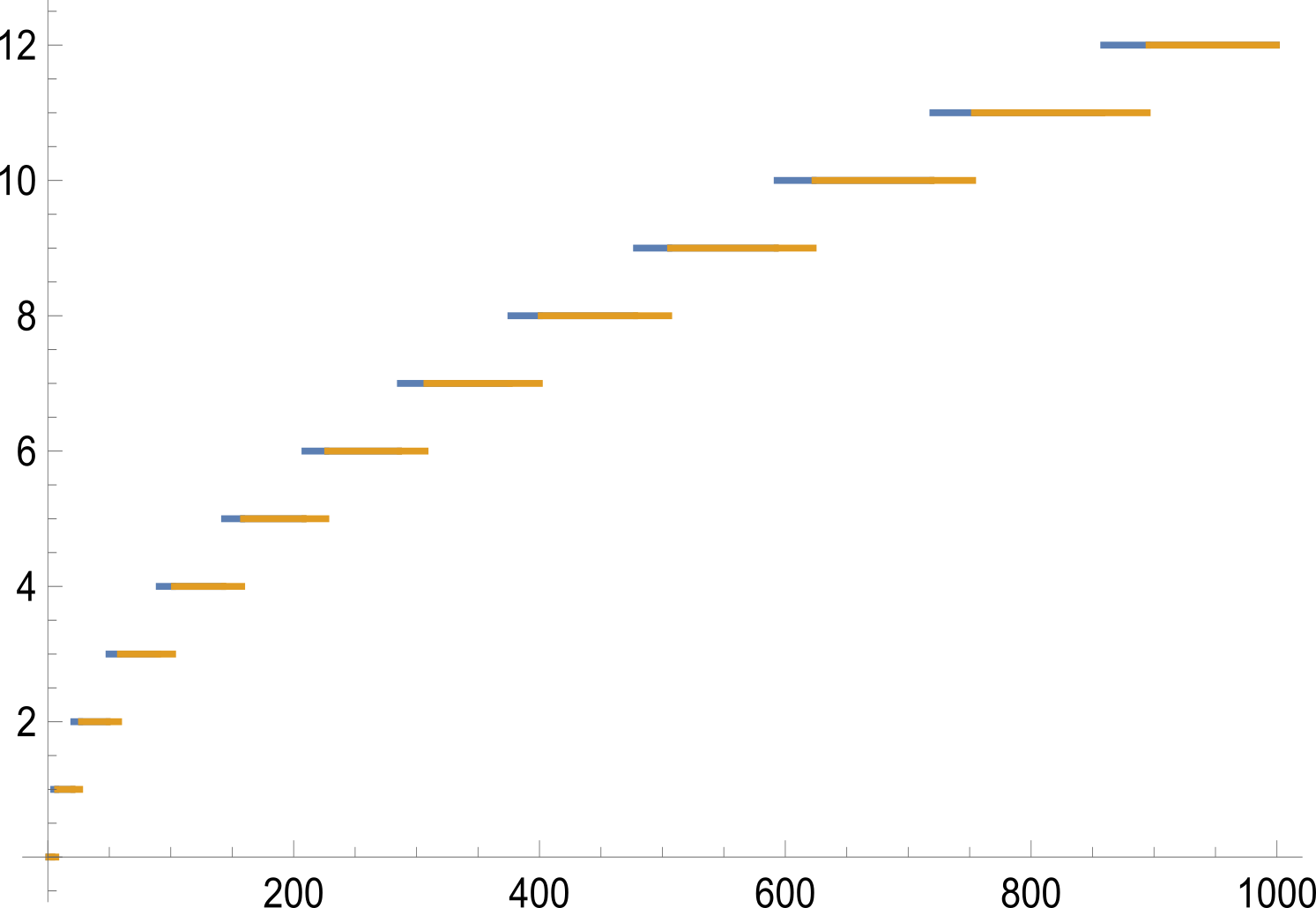

其中黃色表示$2\mid n$的情況，藍色表示$2\nmid n$的情況。
同時可以作出$k=\sqrt{2(c+d)+1/4}-1/2$的圖：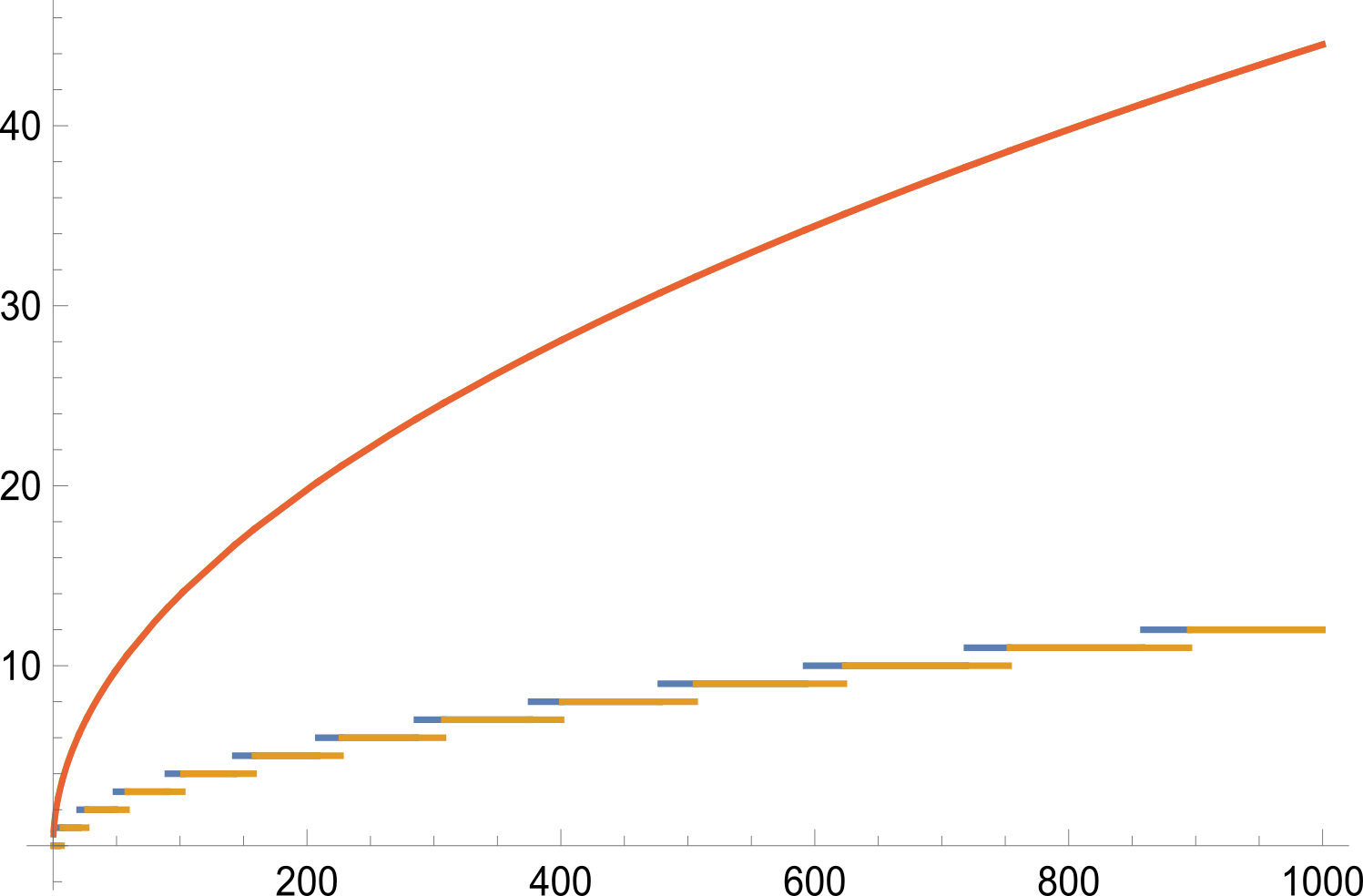

這裡的$k=a_k-a_{k-1}$，因為$d$的上界始終小於$k$，所以$a_{k-1}<b_n<a_{k}$，且$S_n<S_k$的情況始終存在。

於是得出結論：
$$
d_{max}=\begin{cases}
\lfloor-\frac{\sqrt{3}}{2}\cdot\sqrt{\left(14-8 \sqrt{3}\right) c+\left(22 \sqrt{3}-38\right) \sqrt{c}-15 \sqrt{3}+26}+\left(\sqrt{3}-1\right) \sqrt{c}-2 \sqrt{3}+\frac{7}{2}\rfloor,\quad 2\mid n\\
\lfloor\sqrt{3c+3/4}-\sqrt{c+1/4}-\frac{\sqrt{2}}{4}\cdot\sqrt{-4 \sqrt{3} (4 c+1)+8 (4 c+1)+52 c-32 \sqrt{3} c+66 \sqrt{3} \sqrt{4 c+1}-114 \sqrt{4 c+1}-98 \sqrt{3}+169}-2\sqrt{3}+\frac{15}{4}\rfloor,\quad 2\nmid n
\end{cases}
$$
當$a_{k-1}<c=b_n=a_k-d(d\in\mathbb{N^+})$時，若$d\le d_{max}$，則$S_k<S_n$，最小外切三角形選擇稍大的三角形對應的全三角形。
但這個結論其實沒什麼意思，式子太復雜了(而且實際上也是近似解)，對於這種處處取整的問題，不需要這麼高的精度，希望接下來能找到更簡單的表達式。

3. 回歸幾何

除去特殊情況，其他情況也需考慮，這就需要回歸幾何，具體情況具體分析了。
首先選一個三角形數，這裡就選15吧，作出對應的全三角形，然後去掉3個圓，作出如圖所示的12個圓的外切三角形：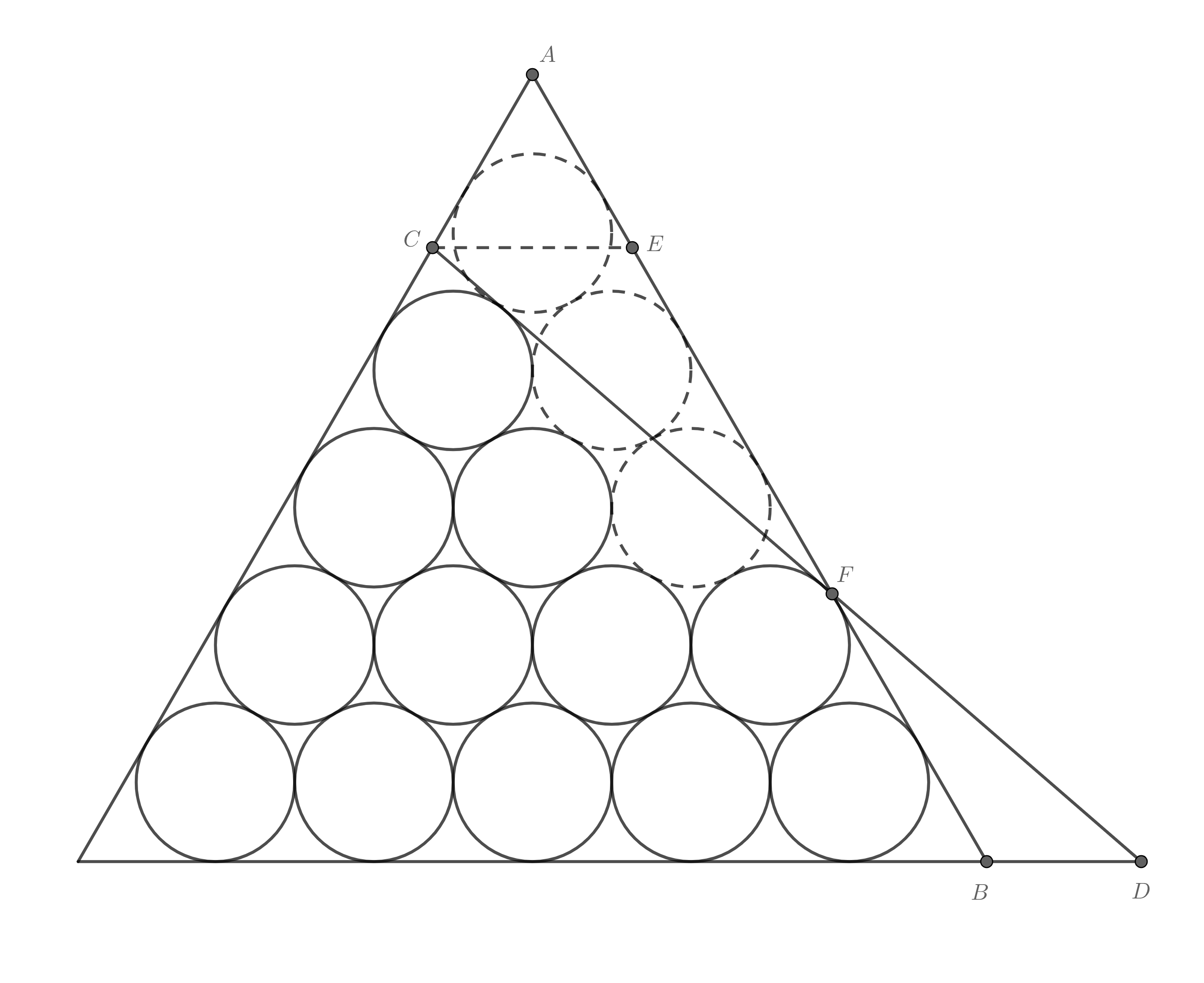

顯然，$\triangle BFD\sim\triangle EFC$，且$BF<EF$，所以$S_{\triangle BFD}<S_{\triangle EFC}$，所以此外切三角形面積小於全三角形。容易得到$CD$的斜率$k=-\sqrt3/2$，然後進行一些計算，最後得到面積為：
$$S=15+\frac{275}{18}\sqrt{3}+3\sqrt{7}+\frac{5}{9}\sqrt{21}\approx51.945,(c=12)$$
而全三角形面積$S_{k}=24+19\sqrt{3}\approx56.909,(a_k=15)$，大於此外切三角形面積，可知此外切三角形是這種排列方式下最小的外切三角形。
但半三角形面積$S_{n}=18+39\sqrt3/2\approx51.775,(b_n=12)$，又小於此外切三角形面積。

若再去掉一個圓，用同樣的方法構造外切三角形：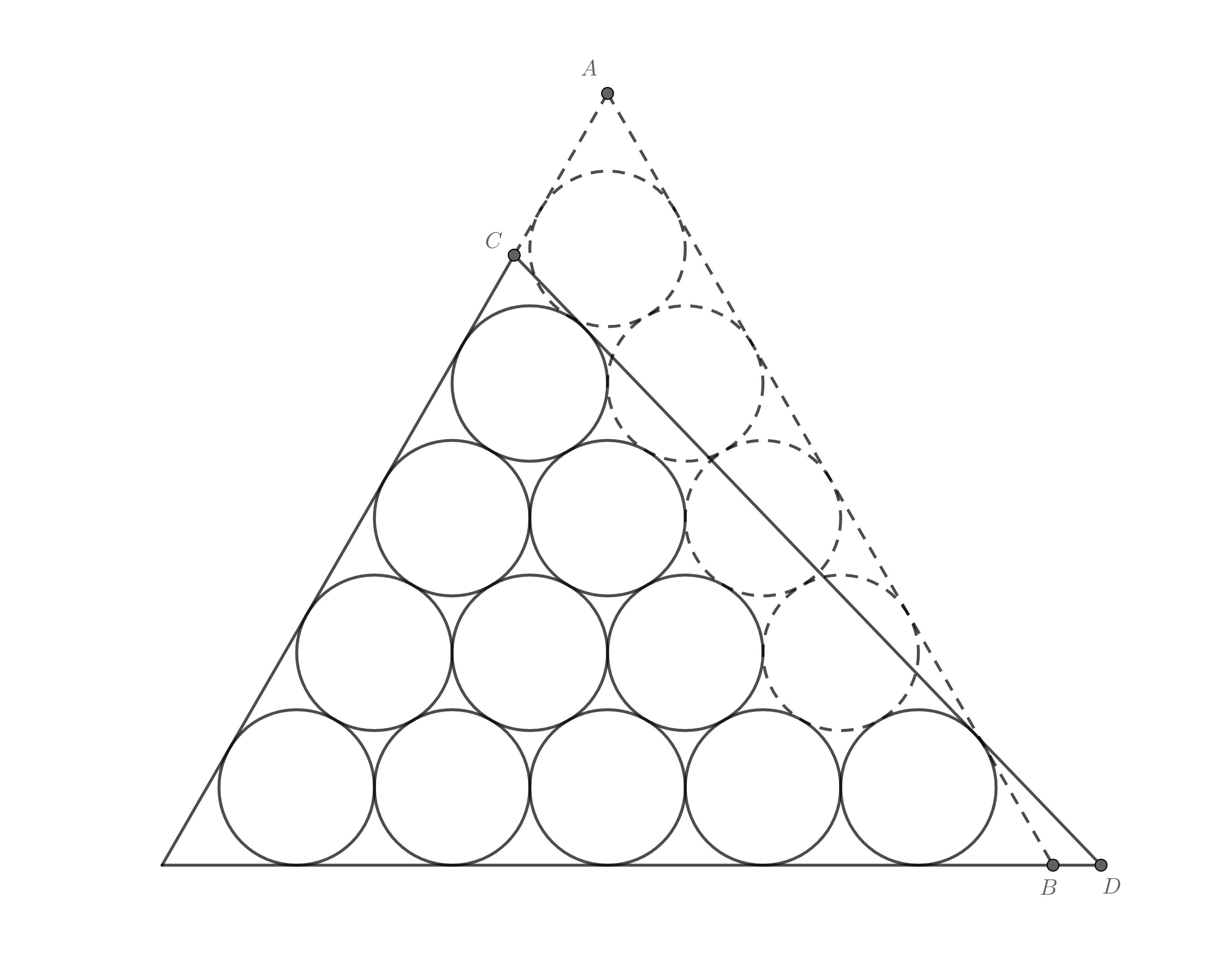

面積明顯又減小了很多，可以用相同的方法計算面積，但計算實在太煩了，就直接用GeoGebra的近似值吧：$S\approx47.407,(c=11)$，這樣得到的面積不僅小於全三角形，而且小於半三角形。
於是得到結論：當$a_{k-1}<c<a_k-k/2$時，存在比全三角形更小的外切三角形(上述情況)，但這種情況下面積似乎沒有通用公式。至於這種情況和可行的半三角形哪個大，就又是一個困難的問題了。(感覺坑越來越大了)