多个圆的最小外切三角形-2

1. 回顾

还是继续对等大情况的研究。
算了一下上一篇所说的两个数列，并分别计算比较了对应的面积，于是记录一下研究进展。
为方便起见，接下来直接称三角形数个圆的外切等边三角形为全三角形，半三角形数个圆的外切直角三角形为半三角形(虽然这个定义很奇怪，名称更奇怪，但是Who cares？)。三角形数和半三角形数分别用$a_k,b_n$表示，圆的个数用$c$表示。

现在有两个数列：

1. 三角形数：
   $$a_k=k(k+1)/2$$
2. 半三角形数：
   $$
   b_n=\begin{cases}
   n^2/4,\quad 2\mid n\\
   (n^2-1)/4,\quad 2\nmid n
   \end{cases}
   $$

在上一篇中以提出猜想：当圆的数目恰为三角形数时，最小外切三角形即为圆按照平面六角密堆积式排列之外切等边三角形(全三角形)；当圆的数目恰为半三角形数时，最小外切三角形即为圆按照类似方法排列之外切直角三角形(半三角形)。如图所示：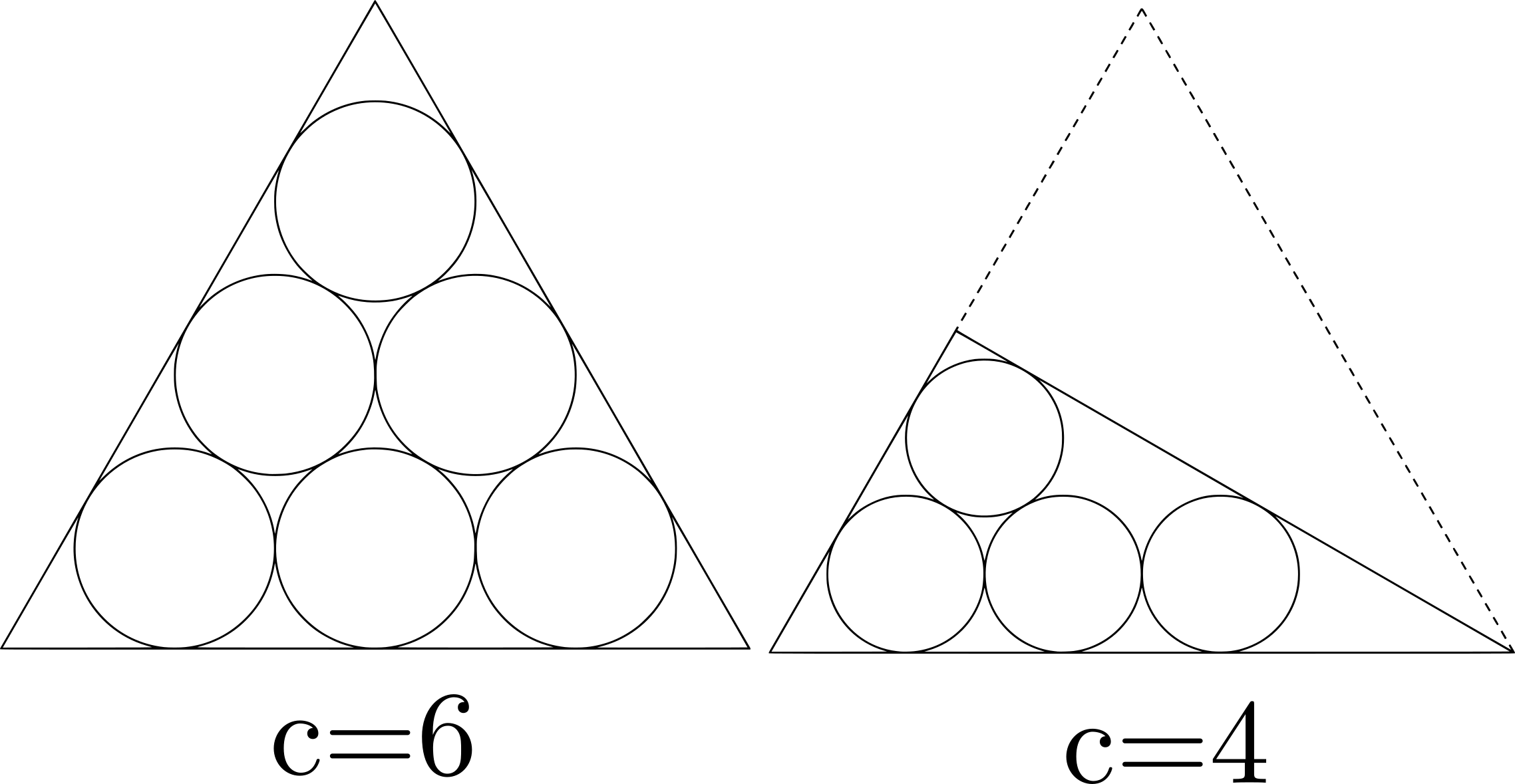

同时，这两种形式的三角形面积可以用$n$和$k$表示：
当$c=a_k$时，
$$S_k=\sqrt{3}k^2+(6-2\sqrt{3})k+4\sqrt{3}-6$$
当$c=b_n$时，
$$S_n=\frac{\sqrt{3}}{2}n^2+(3-\sqrt{3})n+2\sqrt{3}-3$$
此时问题转化成了对这两个数列的研究(似乎已经不是几何问题了)。

2. 对数列的探究

粗略观察两组数列，会发现$k=n$时，$a_k\approx2b_n$，$S_k=2S_n$；两组数值分布不均，但基本在两个三角形数之间存在1至2个半三角形数，同时存在$a_k=b_n$的情况；当$c=b_n=a_k$时，$S_k<S_n$，当$c=b_n<a_k$时，$S_k>S_n$或$S_k<S_n$均有可能。

作出数据图如下，横轴数据为恰是三角形数或半三角形数的圆个数(从4开始)，纵轴为相应的全三角形或半三角形面积，黑色表示全三角形，红色表示半三角形：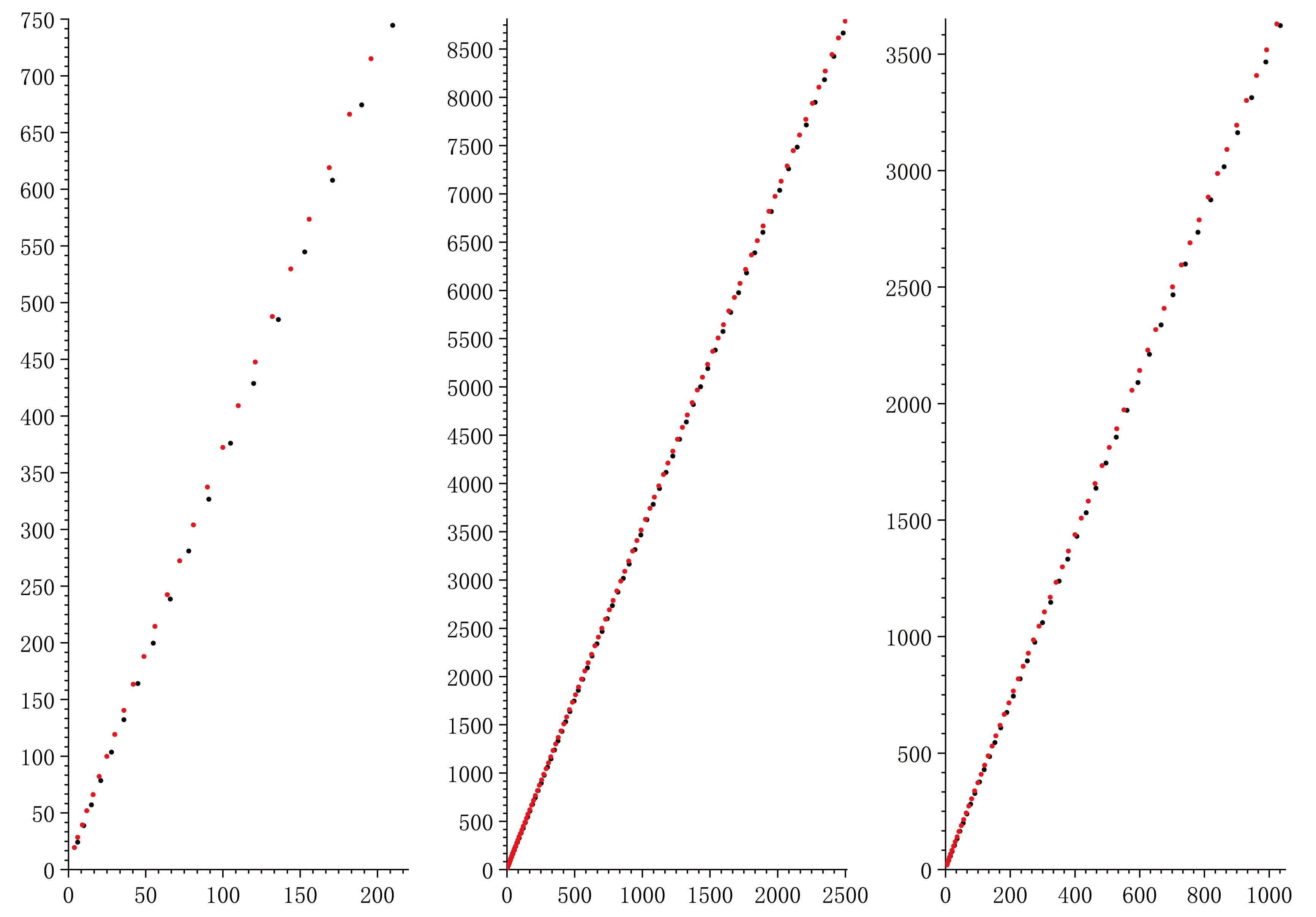

可以看到，面积与圆的数量大致呈正比关系，上述的几个观察结果在图上也反映得很清晰。

首先可以求出数列的递推式：
$$a_{k+1}=a_k+k+1$$
$$
b_{n+1}=\begin{cases}
b_n+n/2,\quad 2\mid n\\
b_n+(n+1)/2,\quad 2\nmid n
\end{cases}
$$
这两个数列的递推都很有意思，$a$是从0开始加上连续自然数(实际数列从1开始)，$b$也是从0开始加连续自然数，但每个自然数加两次。

相等的情况

要研究两个数列数值的大小关系，可以从某一个相等的值开始考虑。
设$a_k=b_n$，则可以得到$n$与$k$的关系：$① n=\sqrt{2k^2+2k}$或$②n=\sqrt{2k^2+2k+1}$，这两个式子包含了$n$的奇偶性信息，由于$k$是整数，①式得到的$n$必然是偶数，②式得到的$n$必然是奇数。但是两式中$k$的奇偶性没有限制，前4组$n$与$k$为：
$$
\begin{align*}
5&=\sqrt{2\times3^2+2\times3+1}\\
12&=\sqrt{2\times8^2+2\times8}\\
29&=\sqrt{2\times20^2+2\times20+1}\\
70&=\sqrt{2\times49^2+2\times49}
\end{align*}
$$
整体观察数据，发现
$$
\begin{align*}
2\nmid n,\quad2\nmid k\\
2\mid n,\quad2\mid k\\
2\nmid n,\quad2\mid k\\
2\mid n,\quad2\nmid k
\end{align*}
$$
这4种情况周期性出现。

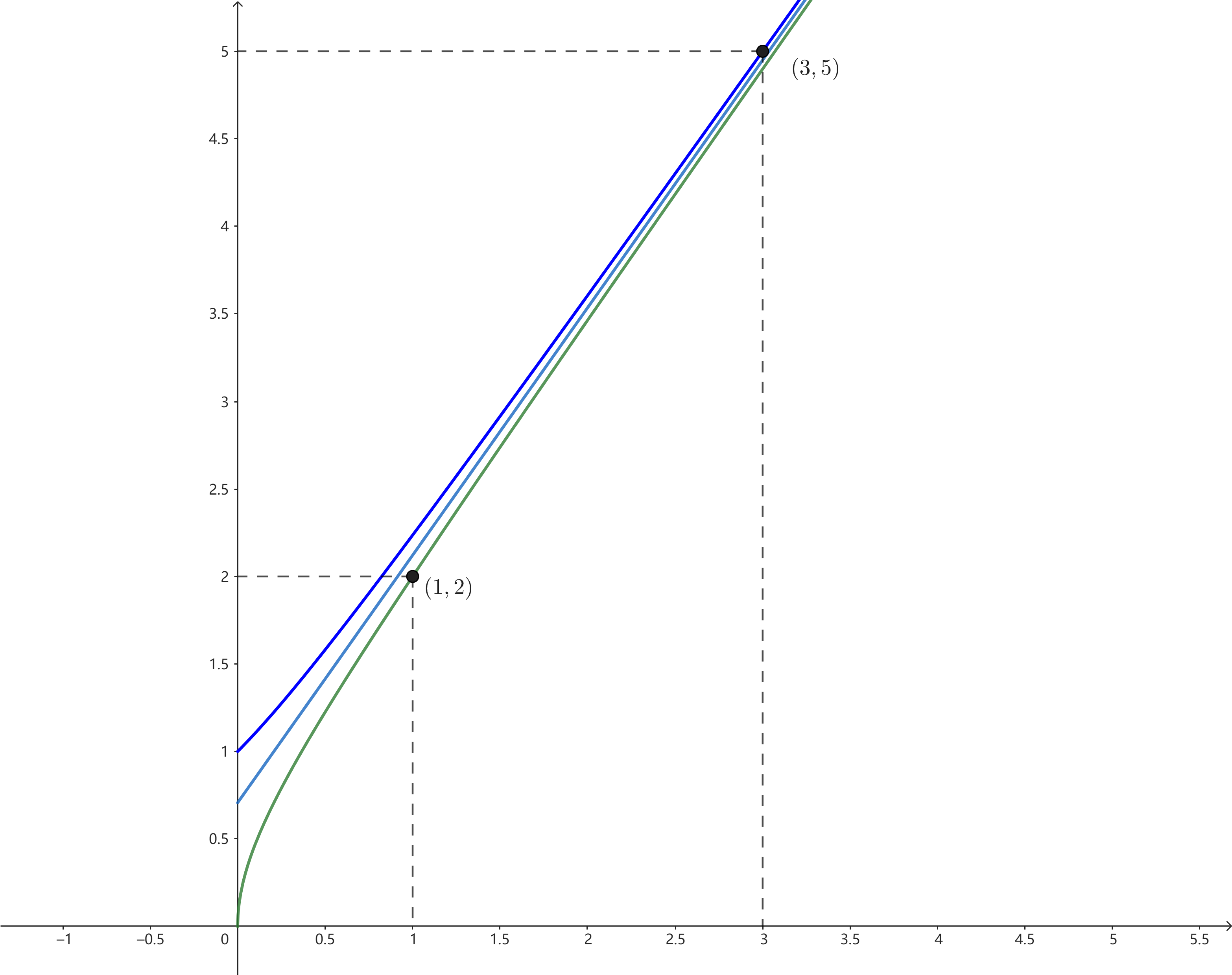如图，$\sqrt{2x^2+2x}$和$\sqrt{2x^2+2x+1}$是$\sqrt2(x+1/2)$的两条渐近线，而一组$n$与$k$就表示这两条渐近线上的一个整点(整点$(1,2)$不算)。这似乎与$\sqrt2$的连分数表示有关系，结论应该可以用相关知识证明，但我对数论了解不多，就不继续了。 显然，由于两条渐近线上的整点是无穷多的，$a_k=b_n$的数量也是无穷的，但出现间隔越来越大。

一些递推

当$a_k=b_n$时，写出$n$和$k$关于$a_k$和$b_n$的关系式：
$$k=\sqrt{2a_k+1/4}-1/2$$
$$
n=\begin{cases}
2\sqrt{b_n},\quad 2\mid n\\
2\sqrt{b_n+1/4},\quad 2\nmid n
\end{cases}
$$
代入递推式：
$$a_{k+1}=a_k+\sqrt{2a_k+1/4}+1/2$$
$$
b_{n+1}=\begin{cases}
b_n+\sqrt{b_n},\quad 2\mid n\\
b_n+\sqrt{b_n+1/4}+1/2,\quad 2\nmid n
\end{cases}
$$
因为$a_k=b_n$，所以$\sqrt{2a_k+1/4}+1/2>\sqrt{b_n}$，$\sqrt{2a_k+1/4}+1/2>\sqrt{b_n+1/4}+1/2$，可知$b_{n+1}<a_{k+1}$。将这个结果再代回递推式，又可以得到$b_{n+2}<a_{k+2}$。当然，这些都是显而易见的，比较$b_{n+2}$和$a_{k+1}$的大小则计算稍繁琐，
$$
b_{n+2}=\begin{cases}
b_n+\sqrt{b_n}+\sqrt{b_n+\sqrt{b_n}+1/4}+1/2,\quad 2\mid n\\
b_n+\sqrt{b_n+1/4}+\sqrt{b_n+\sqrt{b_n+1/4}+1/2}+1/2,\quad 2\nmid n
\end{cases}
$$
因为$a_k=b_n>0$，所以：
$$
\begin{align*}
\sqrt{2a_k+1/4}&<\sqrt{b_n}+\sqrt{b_n+\sqrt{b_n}+1/4}\\
\sqrt{2a_k+1/4}&<\sqrt{b_n+1/4}+\sqrt{b_n+\sqrt{b_n+1/4}+1/2}
\end{align*}
$$
所以$b_{n+2}>a_{k+1}$。
若条件改为$a_k<b_n$，根据上式仍能得到$b_{n+2}>a_{k+1}$，于是可知不存在2个三角形数之间存在3个半三角形数的情况，即2个三角形数之间存在1至2个半三角形数。

之后可继续代回递推式计算，比较大小，但计算太复杂，就不算下去了。
直接观察数据可知，当$k=3$，$n=5$时，
$$
\begin{align*}
a_k=b_n\\
a_k<b_{n+1}<a_{k+1}\\
a_{k+1}<b_{n+2}<a_{k+2}\\
a_{k+2}<b_{n+3}<\textcolor{red}{b_{n+4}}<a_{k+3}\\
\cdots
\end{align*}
$$
对其他满足$a_k=b_n$的$k$和$n$，结果也大致如此，这样的规律是否恒成立？何时2个三角形数之间存在2个半三角形数？
比对面积大小，发现当2个三角形数之间存在2个半三角形数时，较小的半三角形数对应面积小于大三角形数对应面积，而较大的半三角形数对应面积大于大三角形数对应面积，是否必然如此？
这些问题留到以后考虑吧。

比较面积

接下来写出$S_k$和$S_n$与$c$的关系式。
若$c=a_k=k(k+1)/2$，则$k=\sqrt{2a_k+1/4}-1/2$，代入到面积公式中：
$$S_k=2\sqrt3a_k+(6-3\sqrt3)\sqrt{2a_k+1/4}+11\sqrt3/2-9$$
若$c=b_n$，则
$$
n=\begin{cases}
2\sqrt{b_n},\quad 2\mid n\\
2\sqrt{b_n+1/4},\quad 2\nmid n
\end{cases}
$$
代入到面积公式：
$$
S_n=\begin{cases}
2\sqrt3b_n+(6-2\sqrt3)\sqrt{b_n}+2\sqrt3-3,\quad 2\mid n\\
2\sqrt3b_n+(6-2\sqrt3)\sqrt{b_n+1/4}+5\sqrt3/2-3,\quad 2\nmid n
\end{cases}
$$
本来以为这两条曲线也是某条曲线的渐近线，但其实两个函数差的极限是$\sqrt{3}/2$，并不是渐近线。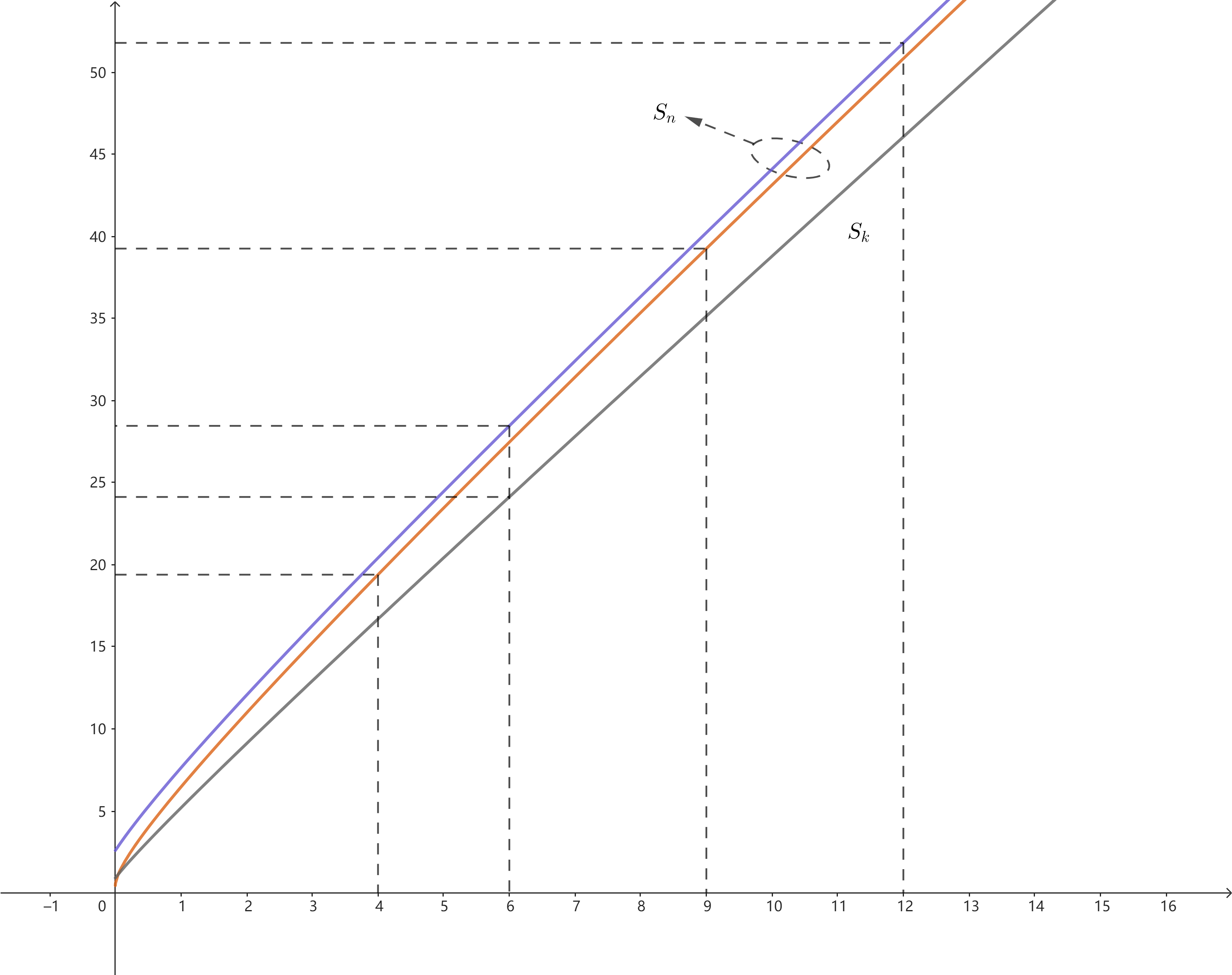

这张图清晰的反映了面积与圆数量的接近正比的关系($1/2$次项几乎可忽略)，并且这条曲线斜率很大(注意图中横纵坐标比值是$1:4$)。

先看最简单的情况：$c=a_k=b_n$，设：
$$
f(c)=S_n-S_k=\begin{cases}
(6-2\sqrt3)\sqrt{c}-(6-3\sqrt3)\sqrt{2c+1/4}-7\sqrt3/2+6,\quad 2\mid n\\
(6-2\sqrt3)\sqrt{c+1/4}-(6-3\sqrt3)\sqrt{2c+1/4}-3\sqrt3+6,\quad 2\nmid n
\end{cases}
$$
若$2\mid n$，当$c>0.04348\cdots$时，$f(c)>0$；若$2\nmid n$，$f(c)$恒大于0.
所以当$c=a_k=b_n$，$S_k<S_n$

关键问题是$a_{k-1}<c=b_n=a_k-d(d\in\mathbb{N^+})$，而$S_k<S_n$的情况，设：
$$
g(c,d)=S_n-S_k=\begin{cases}
-2\sqrt3d+(6-2\sqrt3)\sqrt{c}-(6-3\sqrt3)\sqrt{2(c+d)+1/4}-7\sqrt3/2+6,\quad 2\mid n\\
-2\sqrt3d+(6-2\sqrt3)\sqrt{c+1/4}-(6-3\sqrt3)\sqrt{2(c+d)+1/4}-3\sqrt3+6,\quad 2\nmid n
\end{cases}
$$
理论上，解$g(c,d)>0$的不等式，可以得到$d$的范围，但这个方程没那么好解，直接解会得到长得离谱的答案。
那就先画个三维曲面图吧($2\mid n$)：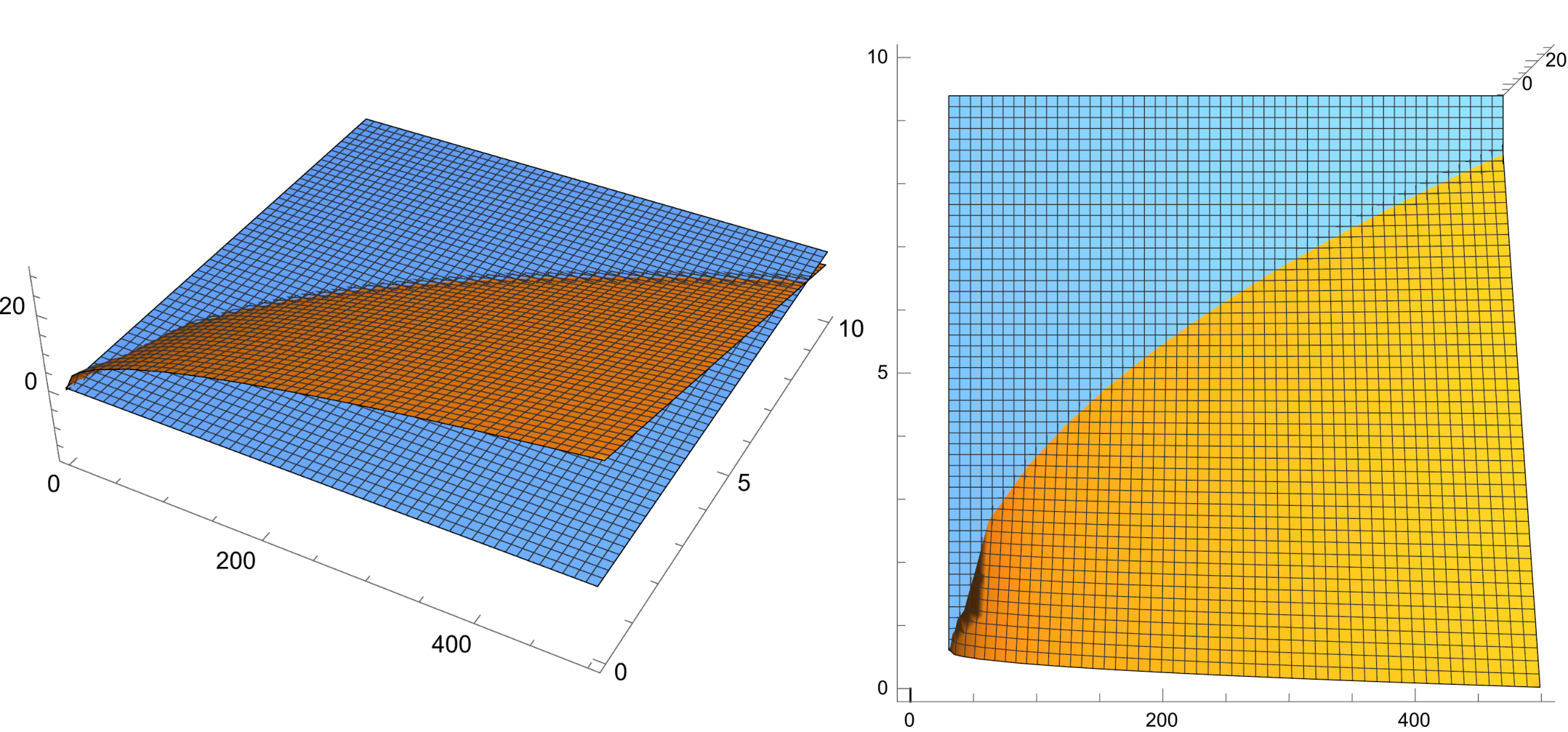

图中黄色的曲面是
$$g(c,d)=-2\sqrt3d+(6-2\sqrt3)\sqrt{c}-(6-3\sqrt3)\sqrt{2(c+d)+1/4}-7\sqrt3/2+6$$
蓝色的曲面是$z=0$，所以黄色曲面在蓝色曲面上的部分就表示不等式$g(c,d)>0$成立的部分。那么要求的就是这两个曲面的交线，曲线以下即使$d$的范围(当然，还有满足$2\mid n$，$c$和$d$取整等条件)。于是直接求解$g(c,d)=0$，神奇的事情发生了，解不等式时的超长答案消失了，取而代之的是两组非常友善的解：
$$
\begin{align*}
d_1&=-\frac{\sqrt{3}}{2}\cdot\sqrt{\left(14-8 \sqrt{3}\right) c+\left(22 \sqrt{3}-38\right) \sqrt{c}-15 \sqrt{3}+26}+\left(\sqrt{3}-1\right) \sqrt{c}-2 \sqrt{3}+\frac{7}{2}\\
d_2&=\frac{\sqrt{3}}{2}\cdot \sqrt{\left(14-8 \sqrt{3}\right) c+\left(22 \sqrt{3}-38\right) \sqrt{c}-15 \sqrt{3}+26}+\left(\sqrt{3}-1\right) \sqrt{c}-2\sqrt{3}+\frac{7}{2}
\end{align*}
$$
但为什么会有两组解？无所谓，直接代回去检验就可以了，发现$d_1$是可行的(其实也有误差，但太小就直接忽略了)。
对$2\nmid n$重复一遍操作，得到(当然，这个其实也是近似的)：
$$d=\sqrt{3c+3/4}-\sqrt{c+1/4}-\frac{\sqrt{2}}{4}\cdot\sqrt{-4 \sqrt{3} (4 c+1)+8 (4 c+1)+52 c-32 \sqrt{3} c+66 \sqrt{3} \sqrt{4 c+1}-114 \sqrt{4 c+1}-98 \sqrt{3}+169}-2\sqrt{3}+\frac{15}{4}$$
这之后还得向下取整，最后得到$1000$以下取整图：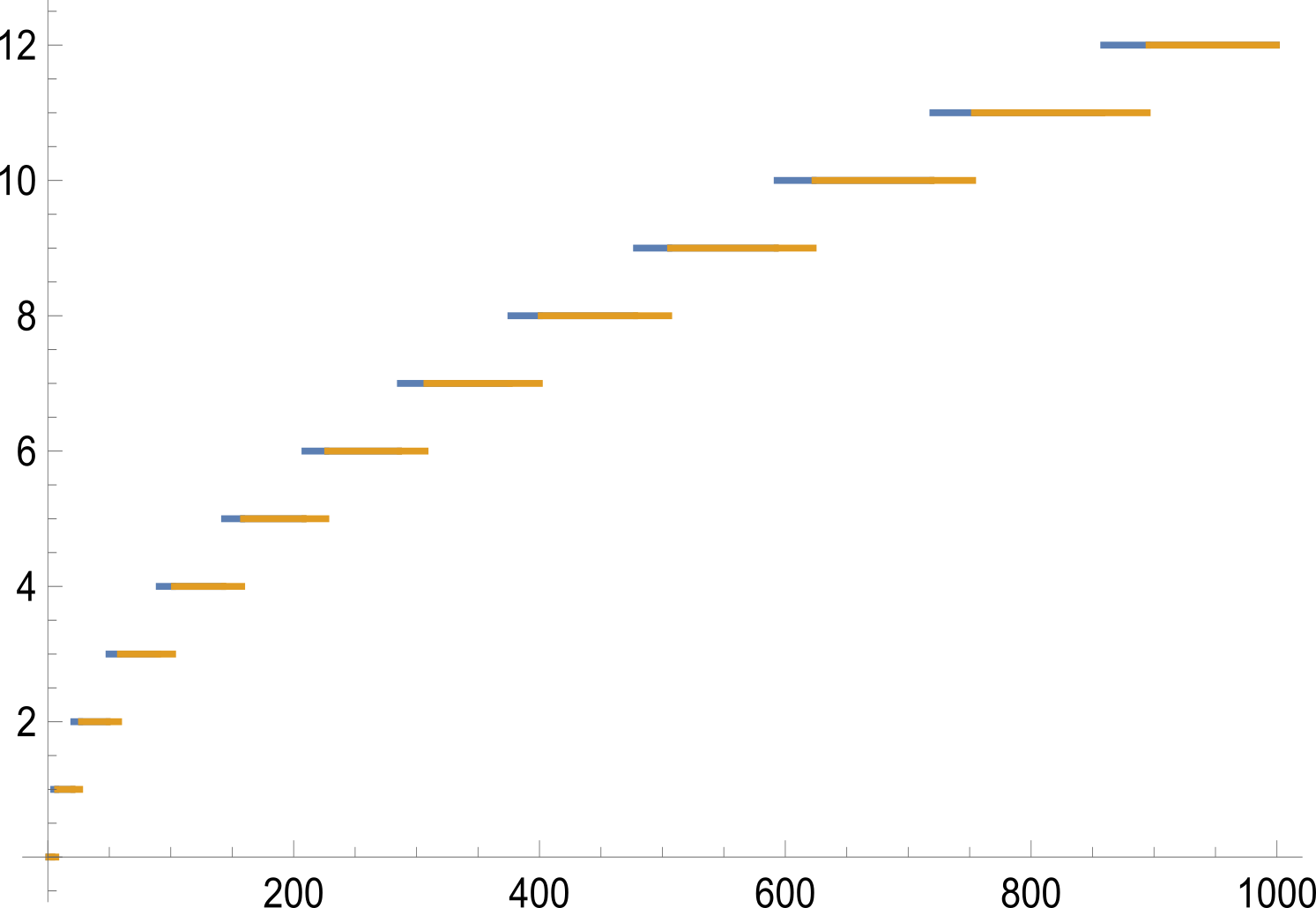

其中黄色表示$2\mid n$的情况，蓝色表示$2\nmid n$的情况。
同时可以作出$k=\sqrt{2(c+d)+1/4}-1/2$的图：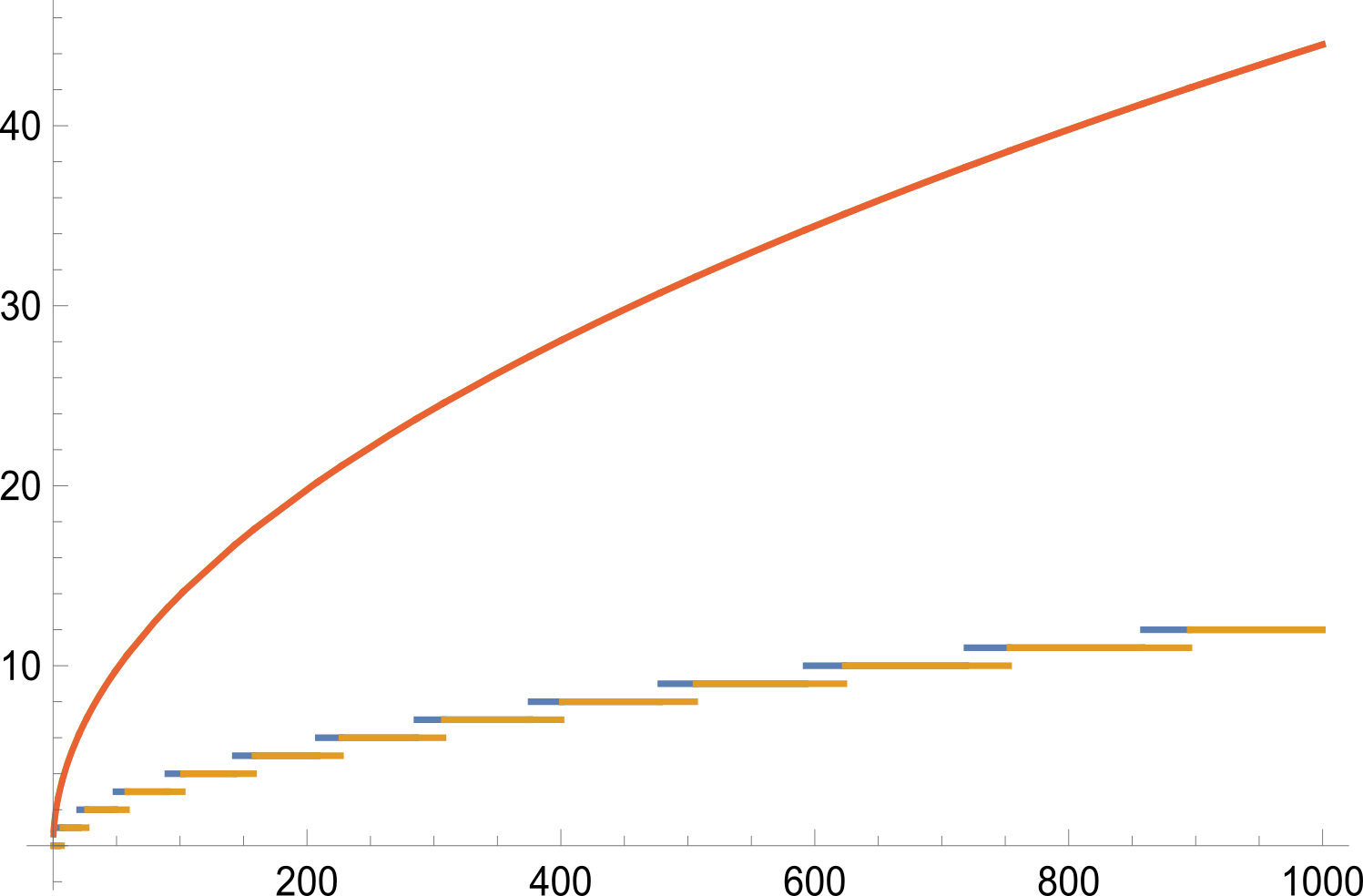

这里的$k=a_k-a_{k-1}$，因为$d$的上界始终小于$k$，所以$a_{k-1}<b_n<a_{k}$，且$S_n<S_k$的情况始终存在。

于是得出结论：
$$
d_{max}=\begin{cases}
\lfloor-\frac{\sqrt{3}}{2}\cdot\sqrt{\left(14-8 \sqrt{3}\right) c+\left(22 \sqrt{3}-38\right) \sqrt{c}-15 \sqrt{3}+26}+\left(\sqrt{3}-1\right) \sqrt{c}-2 \sqrt{3}+\frac{7}{2}\rfloor,\quad 2\mid n\\
\lfloor\sqrt{3c+3/4}-\sqrt{c+1/4}-\frac{\sqrt{2}}{4}\cdot\sqrt{-4 \sqrt{3} (4 c+1)+8 (4 c+1)+52 c-32 \sqrt{3} c+66 \sqrt{3} \sqrt{4 c+1}-114 \sqrt{4 c+1}-98 \sqrt{3}+169}-2\sqrt{3}+\frac{15}{4}\rfloor,\quad 2\nmid n
\end{cases}
$$
当$a_{k-1}<c=b_n=a_k-d(d\in\mathbb{N^+})$时，若$d\le d_{max}$，则$S_k<S_n$，最小外切三角形选择稍大的三角形对应的全三角形。
但这个结论其实没什么意思，式子太复杂了(而且实际上也是近似解)，对于这种处处取整的问题，不需要这么高的精度，希望接下来能找到更简单的表达式。

3. 回归几何

除去特殊情况，其他情况也需考虑，这就需要回归几何，具体情况具体分析了。
首先选一个三角形数，这里就选15吧，作出对应的全三角形，然后去掉3个圆，作出如图所示的12个圆的外切三角形：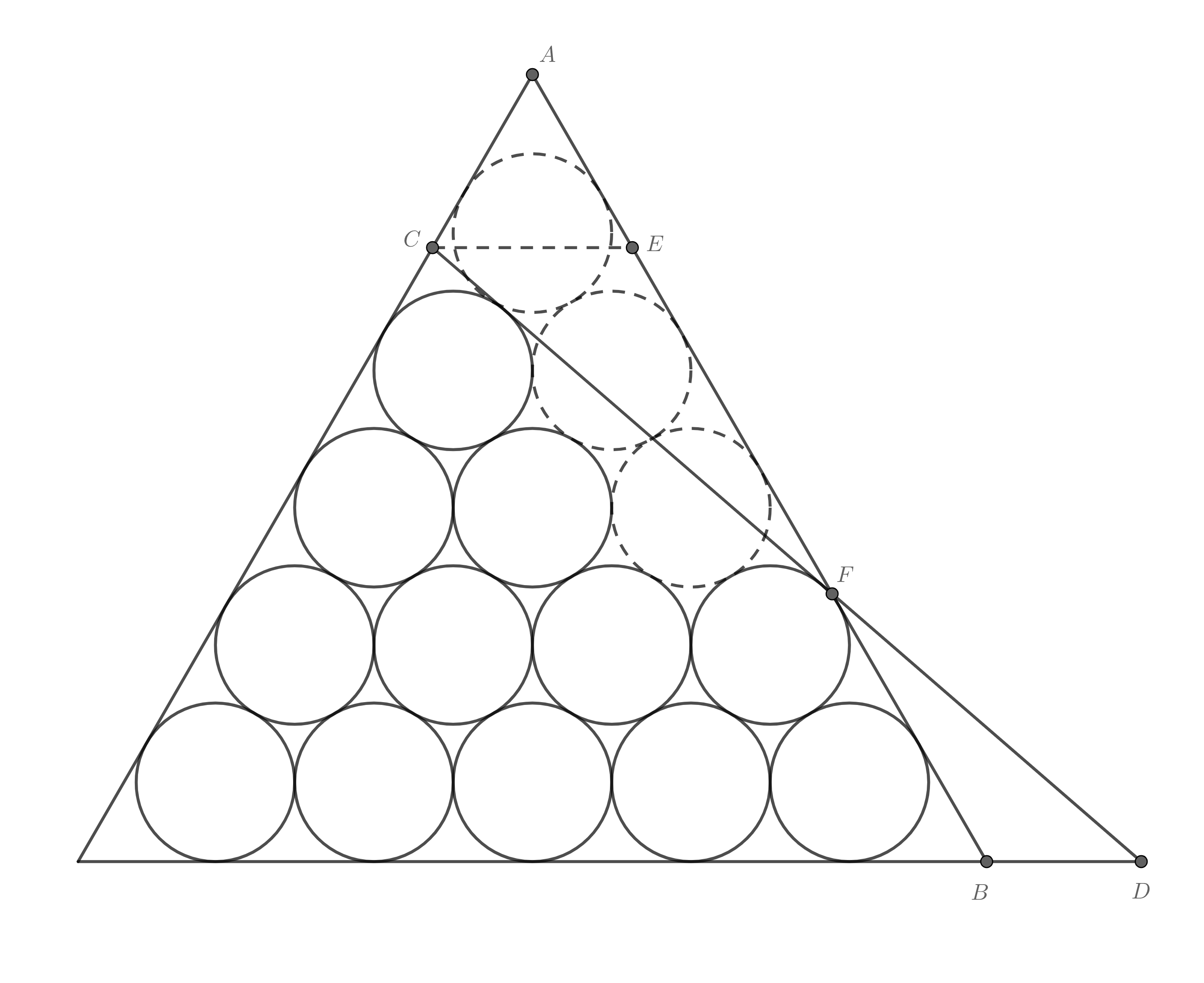

显然，$\triangle BFD\sim\triangle EFC$，且$BF<EF$，所以$S_{\triangle BFD}<S_{\triangle EFC}$，所以此外切三角形面积小于全三角形。容易得到$CD$的斜率$k=-\sqrt3/2$，然后进行一些计算，最后得到面积为：
$$S=15+\frac{275}{18}\sqrt{3}+3\sqrt{7}+\frac{5}{9}\sqrt{21}\approx51.945,(c=12)$$
而全三角形面积$S_{k}=24+19\sqrt{3}\approx56.909,(a_k=15)$，大于此外切三角形面积，可知此外切三角形是这种排列方式下最小的外切三角形。
但半三角形面积$S_{n}=18+39\sqrt3/2\approx51.775,(b_n=12)$，又小于此外切三角形面积。

若再去掉一个圆，用同样的方法构造外切三角形：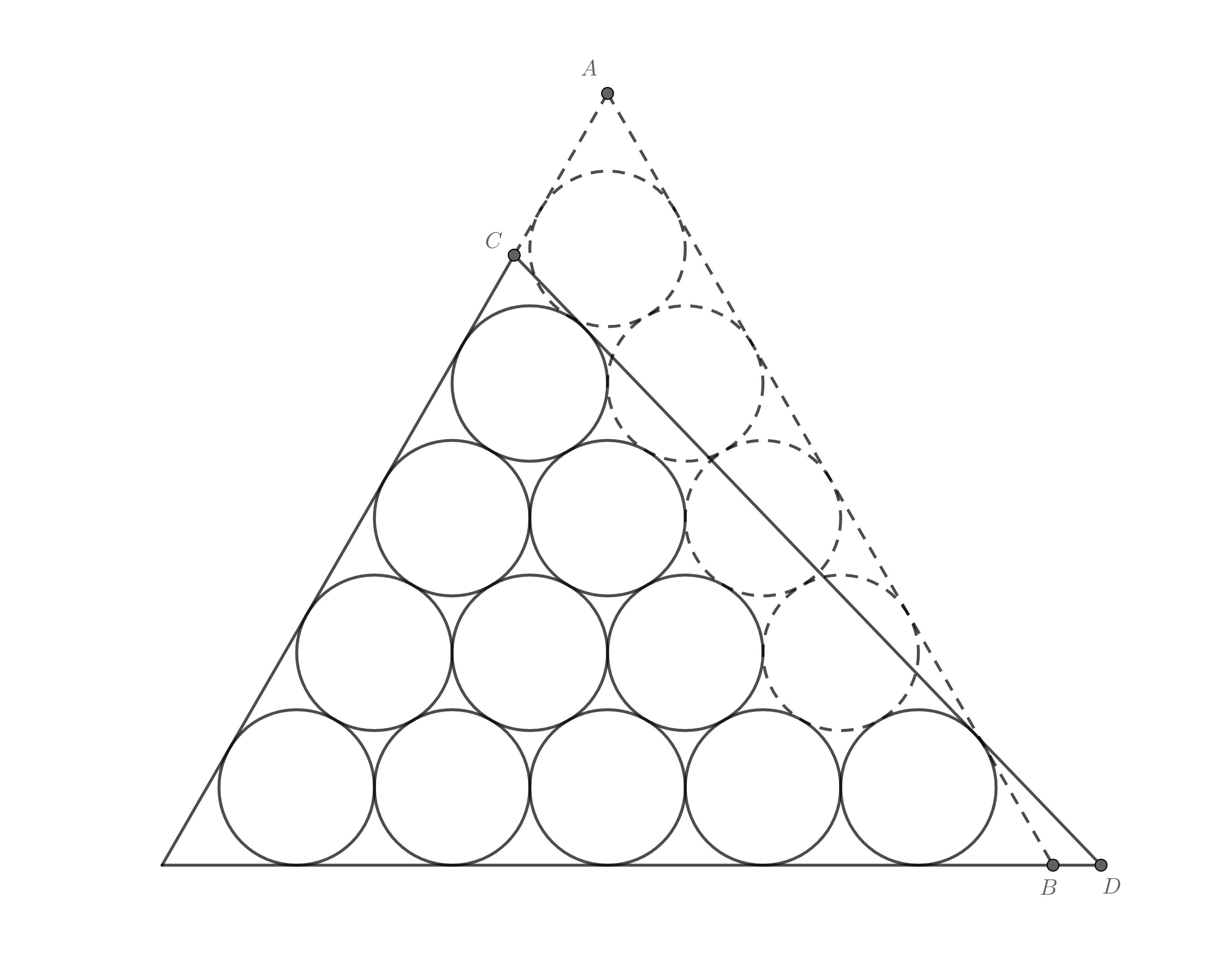

面积明显又减小了很多，可以用相同的方法计算面积，但计算实在太烦了，就直接用GeoGebra的近似值吧：$S\approx47.407,(c=11)$，这样得到的面积不仅小于全三角形，而且小于半三角形。
于是得到结论：当$a_{k-1}<c<a_k-k/2$时，存在比全三角形更小的外切三角形(上述情况)，但这种情况下面积似乎没有通用公式。至于这种情况和可行的半三角形哪个大，就又是一个困难的问题了。(感觉坑越来越大了)