多个圆的最小外切三角形-1
1. 问题
看到一个很有意思的问题:
把面积分别为1,2,3…99,100的100个圆平铺在一个三角形里,这个三角形至少有多大? https://www.zhihu.com/question/612605604
然后我就联想到了这个: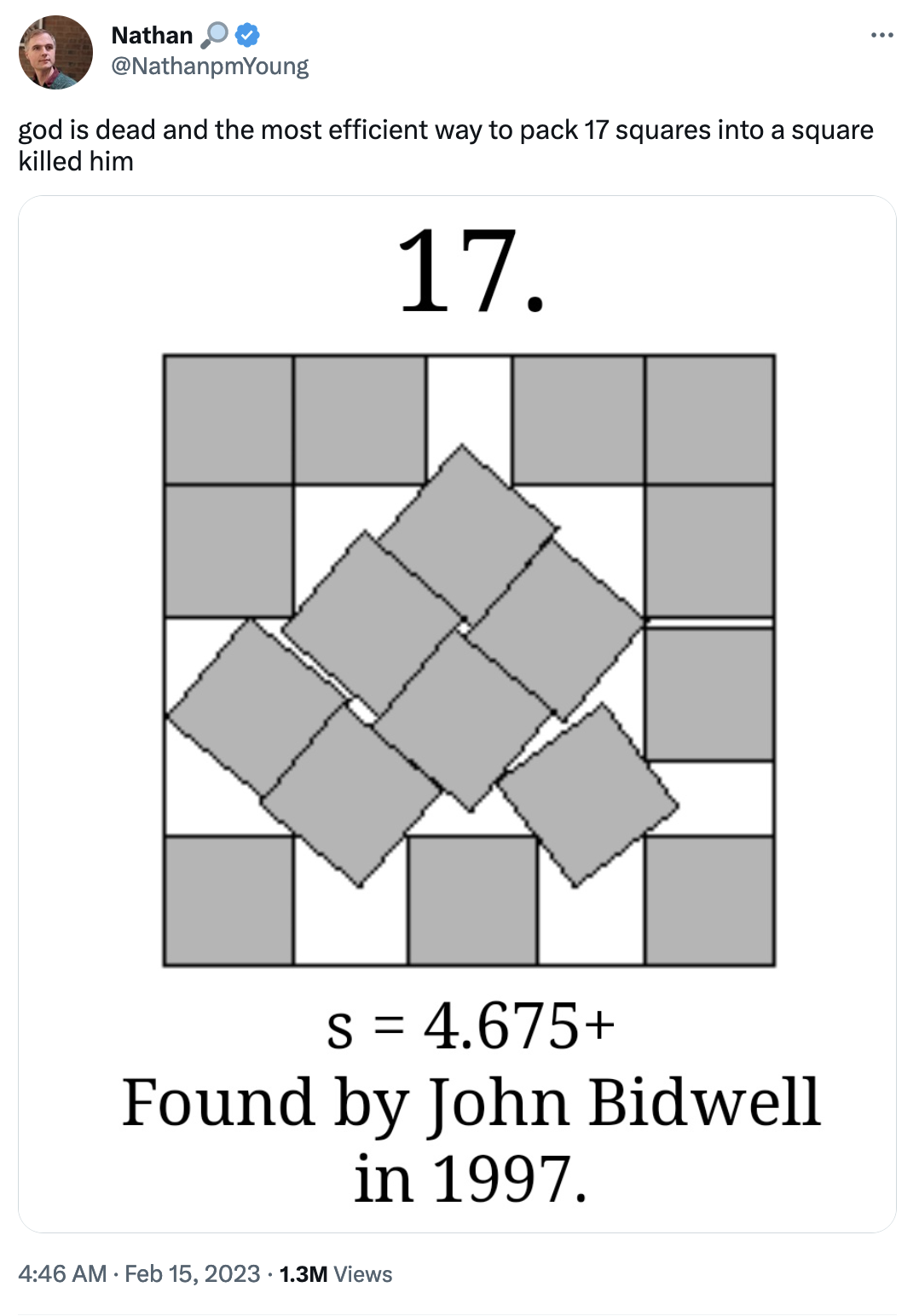
天知道这是怎么算出来的……
这个问题的本质大概就是寻找多个圆的最小外切三角形(显然必须相切,不然就不能最小,且每个圆也最好是相切的),在网上查了一下,没发现什么相关信息g感觉很有趣,那就稍微研究一下。
由于大小不同的圆过于复杂,这里先考虑大小相等的圆。
2. 一个圆
严格证明
先考虑一个圆。
一个圆的外切三角形面积最小值很好求,设圆半径为$r$,三角形三个角为$A,B,C$,对边分别为$a,b,c$,于是$S=1/2\cdot r(a+b+c)$,同时可以用$r$和三个角表示三边:
$$
\begin{aligned}
a=r\cot\frac{B}{2}+r\cot\frac{C}{2}\\
b=r\cot\frac{A}{2}+r\cot\frac{C}{2}\\
c=r\cot\frac{A}{2}+r\cot\frac{B}{2}
\end{aligned}
$$
所以$S=r^2(\cot\frac{A}{2}+\cot\frac{B}{2}+\cot\frac{C}{2})$,余切函数在$(0,\pi/2)$是凸函数,直接用琴生不等式就可以得到:
$$S_{min}=3r^2\cot\frac{A+B+C}{6}=3\sqrt{3}r^2$$
此时$A=B=C$,是等边三角形。
几何直观
虽然使用琴生不等式很简单,但似乎不易推广到多个圆的情况,所以我想到了一种借助几何直观的方法。
当然这种方法很不严格,只是投机取巧的做法罢了,谈不上证明。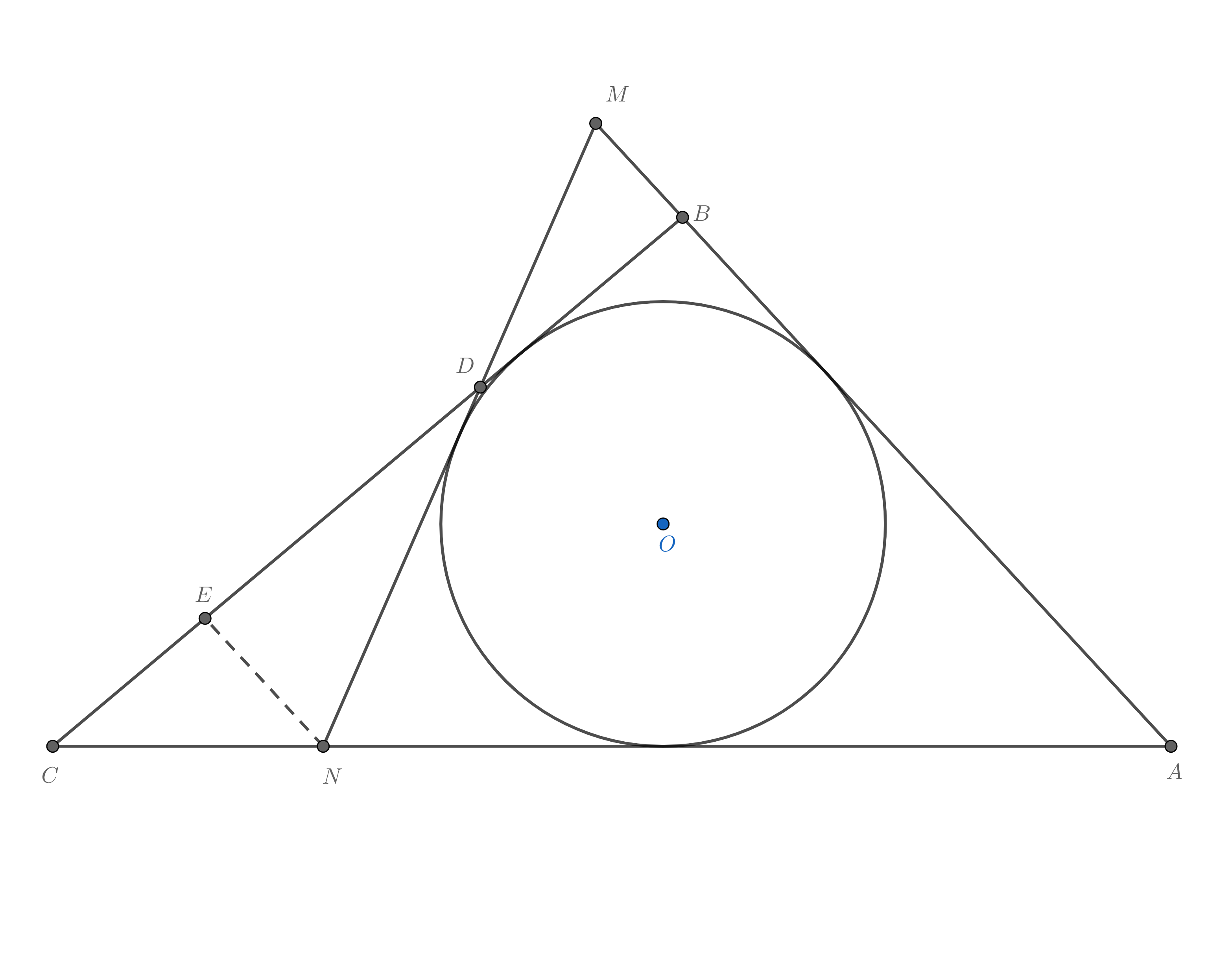
如图,固定两条切线$AC$和$AB$,观察第三条切线$BC$,不妨设$CD>BD$。作圆的切线$MN$,且切点为$MN$中点,作$NE\parallel MB$。
显然$\triangle MDB\sim\triangle NDE$,因为$ND>MD$,所以$S_{\triangle MDB}<S_{\triangle NDE}$,那么$S_{\triangle MDB}<S_{\triangle NDC}$,$S_{\triangle AMN}<S_{\triangle ABC}$,可知$\triangle AMN$面积最小。由于对称性,三边切点都是中点时面积最小,此时外切三角形是等边三角形。
3. 两个圆
分成两种情况考虑,一是一边与两个圆相切,二是三边都只与一个圆相切。(至于为什么是两种,请显然。)
情况一
本来想直接建系算的,但计算太复杂,超出了我的能力范围。(算出来大概也求不了最值)
那就故技重施,取切点为中点的情况: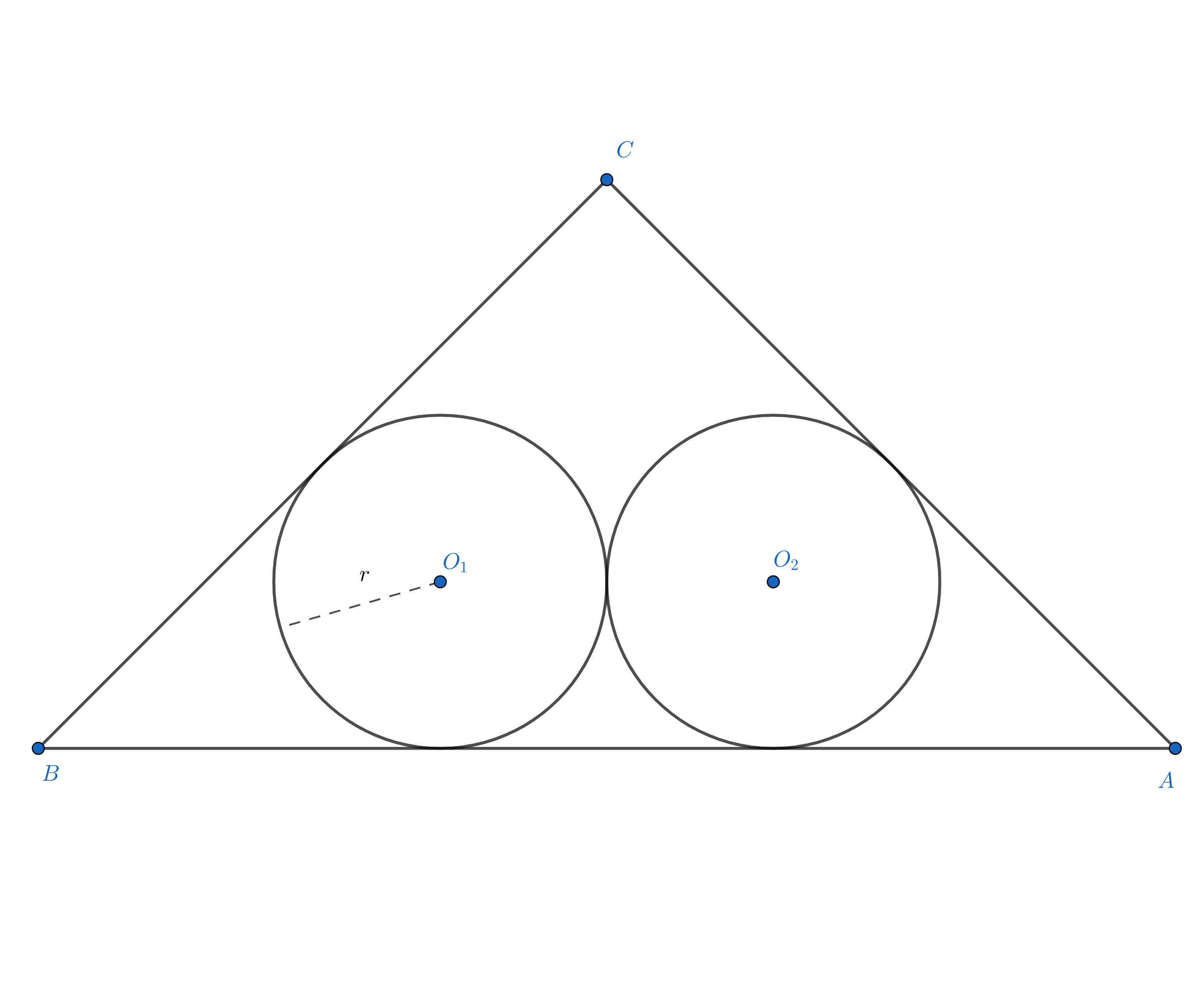
很容易就能看出此时三角形为等腰直角三角形,面积$S=(6+4\sqrt{2})r^2\approx11.657r^2$。
情况二
还是一样的方法,但计算繁琐一些。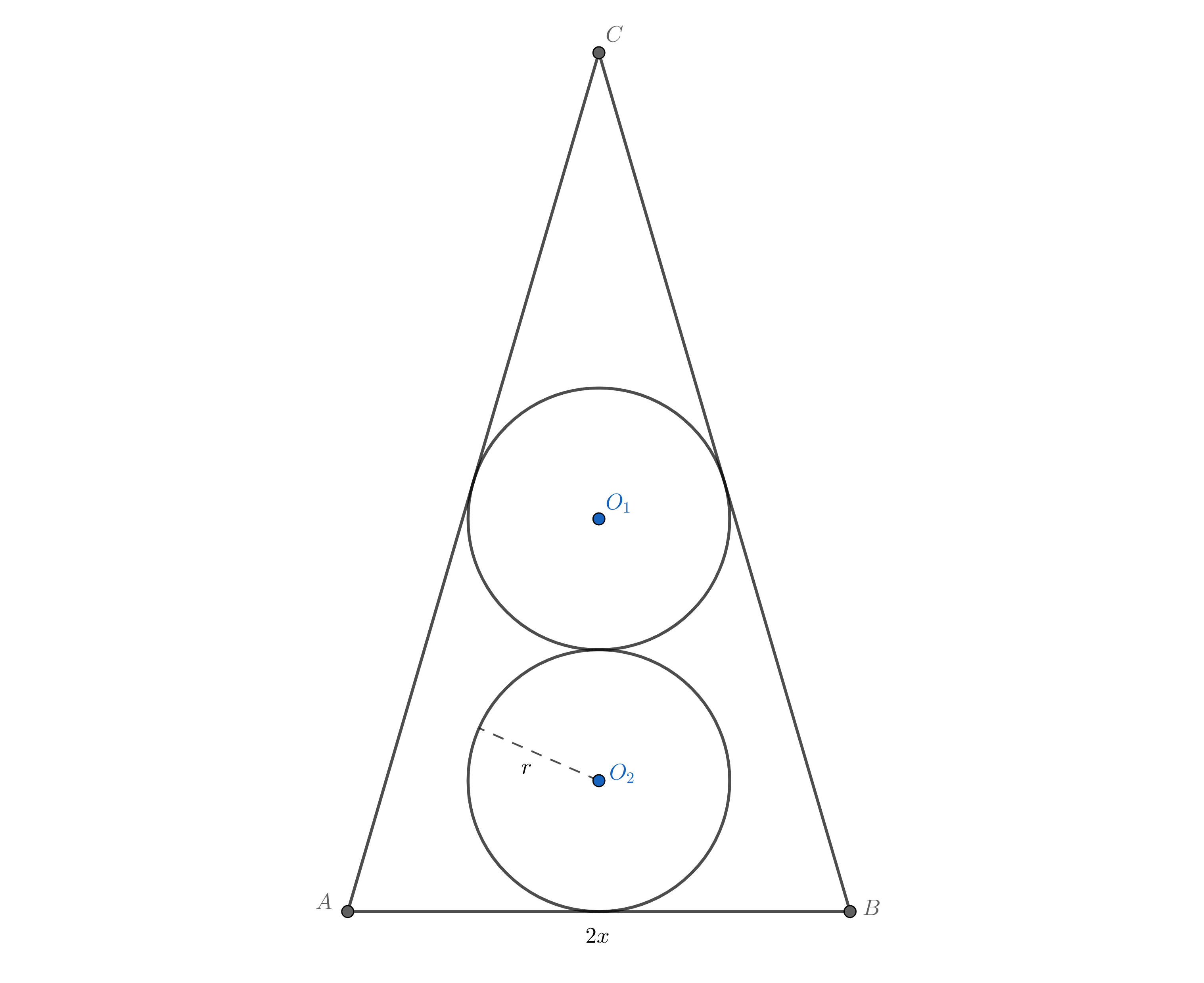
设底边长为$2x$,根据勾股定理列方程:
$$(\sqrt{(3r)^2+x^2}+3r)^2+x^2=(2\sqrt{(3r)^2+x^2-r^2})^2$$
解得$x=\sqrt{\frac{1}{2}(3\sqrt{17}-5)}r$,于是可以算出面积:
$$S=\frac{\sqrt{6\sqrt{17}-10}\cdot(\sqrt{17}+9)}{4}r^2\approx12.595r^2$$
比较
那么就可以对比面积了,显然第一种情况面积更小一些。于是得出结论:两个圆的最小外切三角形是等腰直角三角形,面积最小值$S=(6+4\sqrt{2})r^2$。
虽然不能严格证明,但这确实是我找到的最小了。
还有一个问题是:为什么情况一比情况二面积小?
两种情况都是等腰三角形,可以从中间切开考虑,得到两个直角三角形都包含了一个圆,情况二的空隙更大一些,直觉上说就是这样(唉说了跟没说一样)。
提出猜想1:情况一面积始终比情况二小,且两情况的差距会随圆个数的增加而增加。
4. 三个圆
这里要分3种情况考虑:
- 类似上述情况一
- 类似上述情况二
- 平面六角密堆积式排列,外切等边三角形
从直觉来看,显然情况3是最小的,且情况1小于情况2,但我没有什么简单的比较方法,那就干脆全部算出来好了(顺便锻炼计算能力)。
情况一
直接建系如图,并设圆的半径为1.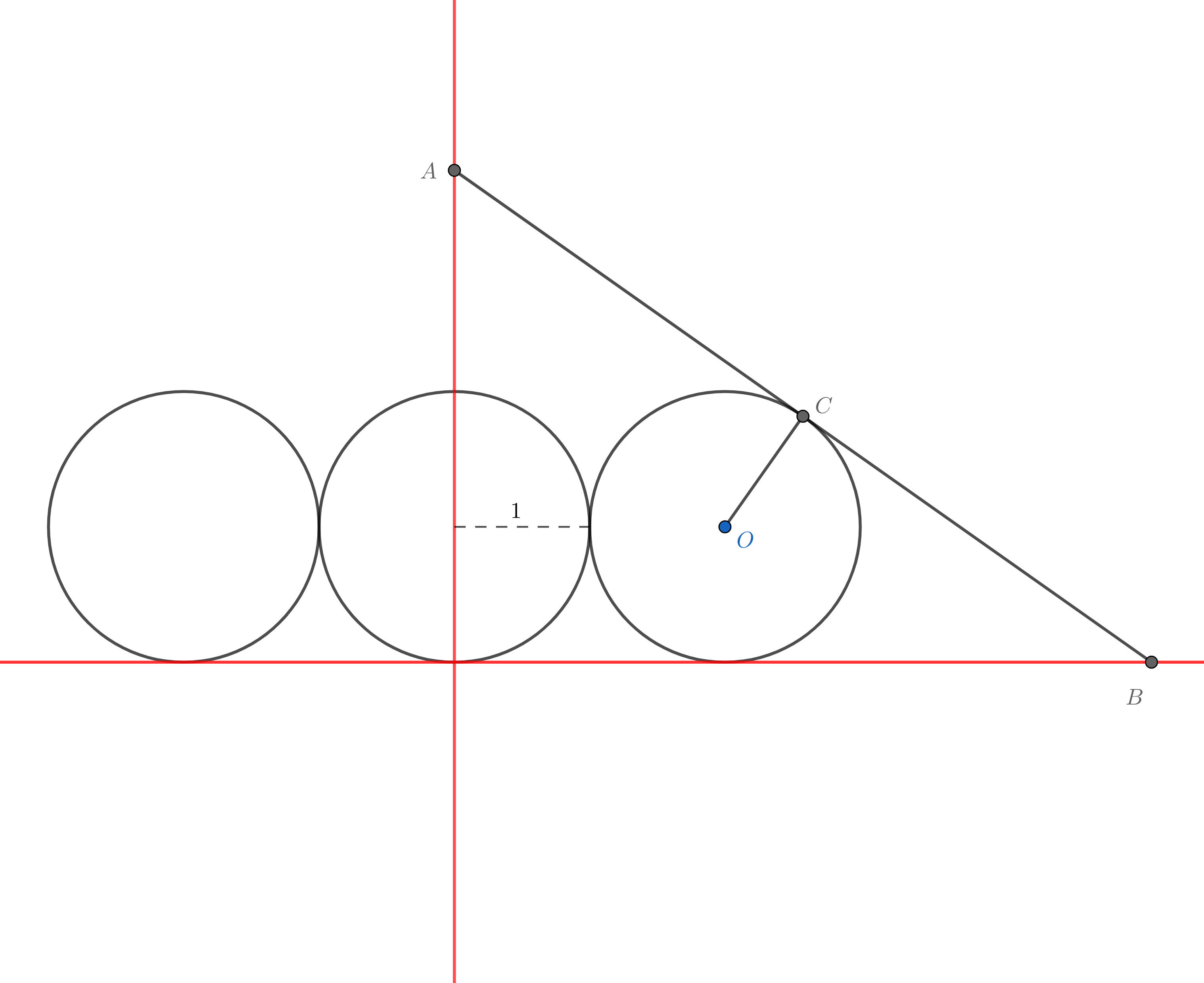
设$A$点坐标$(0,a)$,$B$点$(b,0)$,$AB$中点$C$坐标$(b/2,a/2)$,可得$AB$的解析式:
$$AB:y=-\frac{a}{b}x+a$$
$AB$与圆在$C$点相切时,$OC\perp AB$,由此可以算出$OC$的解析式:
$$OC:y=\frac{b}{a}x+\frac{a^2-b^2}{2a}$$
根据”$OC$过点$O$”和”$C$在圆$O$上”列出方程:
$$
\begin{align*}
2\cdot\frac{b}{a}+\frac{a^2-b^2}{2a}=1\\
(\frac{1}{2}b-2)^2+(\frac{1}{2}a-1)^2=1
\end{align*}
$$
整理一下就出现了喜闻乐见的一元四次方程:
$$x^4-12 x^3+49 x^2-80 x+48=0$$
这、完全不会解。
没关系,还有Wolfram|Alpha,轻松得到答案为:
$$b=\frac{1}{3} \left(\sqrt[3]{3 \sqrt{183}+62}+\sqrt[3]{62-3 \sqrt{183}}+8\right)\approx5.15276$$
继续代回式子,得到:
$$S=ab\approx18.727$$
所以$S\approx18.727r^2$
情况二
这种情况简单许多,和一个圆时类似,设底边为$2x$,根据勾股定理列方程(图都懒得画了):
$$(\sqrt{(5r)^2+x^2}+5r)^2+x^2=(2\sqrt{(5r)^2+x^2-r^2})^2$$
解得$x=\sqrt{\frac{1}{2} \left(5 \sqrt{33}-21\right)}r$,于是算出面积:
$$S=\frac{1}{2} \sqrt{\frac{1}{2} \left(5 \sqrt{33}-21\right)} \left(\sqrt{10 \sqrt{33}+58}+10\right)r^2\approx20.382r^2$$
情况三
看起来很好算,实际上确实很好算。如果建系死算大概会比较复杂,但直接算高$CF$就会轻松很多。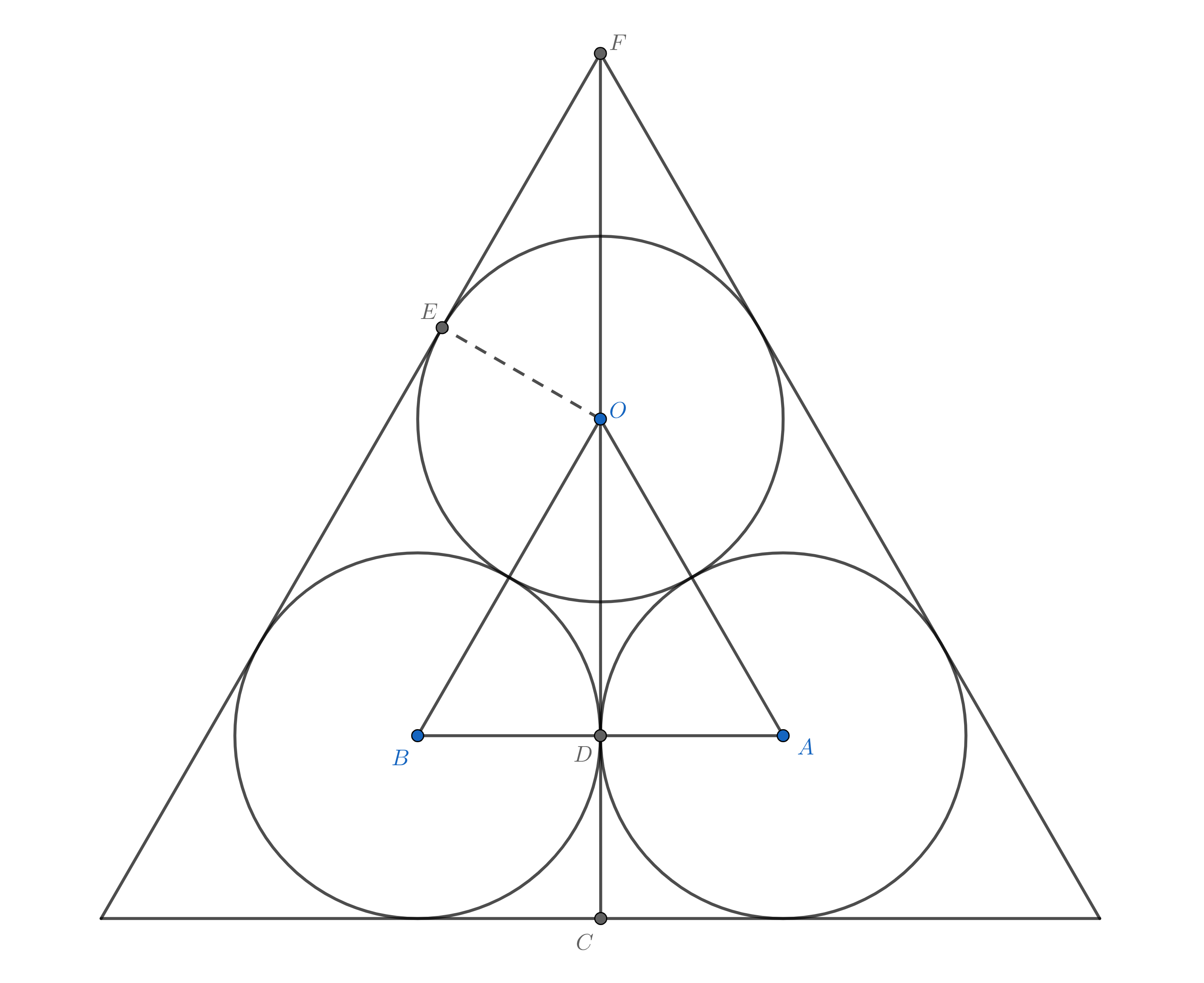
首先易知$CD=r$,然后由于$\triangle OAB$是等边三角形,$OD=\sqrt{3}r$,由于$\triangle OEF$是带60°的直角三角形,$OF=2OE=2r$,所以$CF=3+\sqrt{3}$,容易算出三角形面积:
$$S=(6+4\sqrt{3})r^2\approx12.928r^2$$
比较
到这里,差距就很明显了,情况三显著小于情况一和二,甚至与两个圆的最小外切三角形面积相差无几,看来这的确是一种节省空间的排列方式。因此对于较多的圆,前两种情况可以不用考虑了,差距只会越来越大。
提出猜想2:对于三角形数个圆,最小外切三角形必然是类似情况三的等边三角形。
可以总结出这类三角形的面积公式:
若圆的个数为$k(k+1)/2$,则可算出高为$h=1+2+(k-1)\sqrt{3}=3+(k-1)\sqrt{3}$,由此得到三角形面积$S=\sqrt{3}k^2+(6-2\sqrt{3})k+4\sqrt{3}-6$。
那么需要特别考虑的就是非三角形数个圆的情况。
三角形数:该数目个点或等大圆在等距情况下可排列成三角形,对于相切的等大圆,即可排列成等边三角形的现状。
前10个三角形数为:1, 3, 6, 10, 15, 21, 28, 36, 45, 55
5. 四、五、六
经过以上的探究,总结出两条经验:
- 若某条线段仅与一个圆相切,尽量使切点在切线段的中点
- 尽量排列紧密,最好以平面六角密堆积式排列
接下来对四、五、六个圆的情况进行分析。为方便起见,接下来默认$r=1$。
情况一
六个圆用平面六角密堆积式排列,形成的外切三角形同时也可容纳四个或五个圆: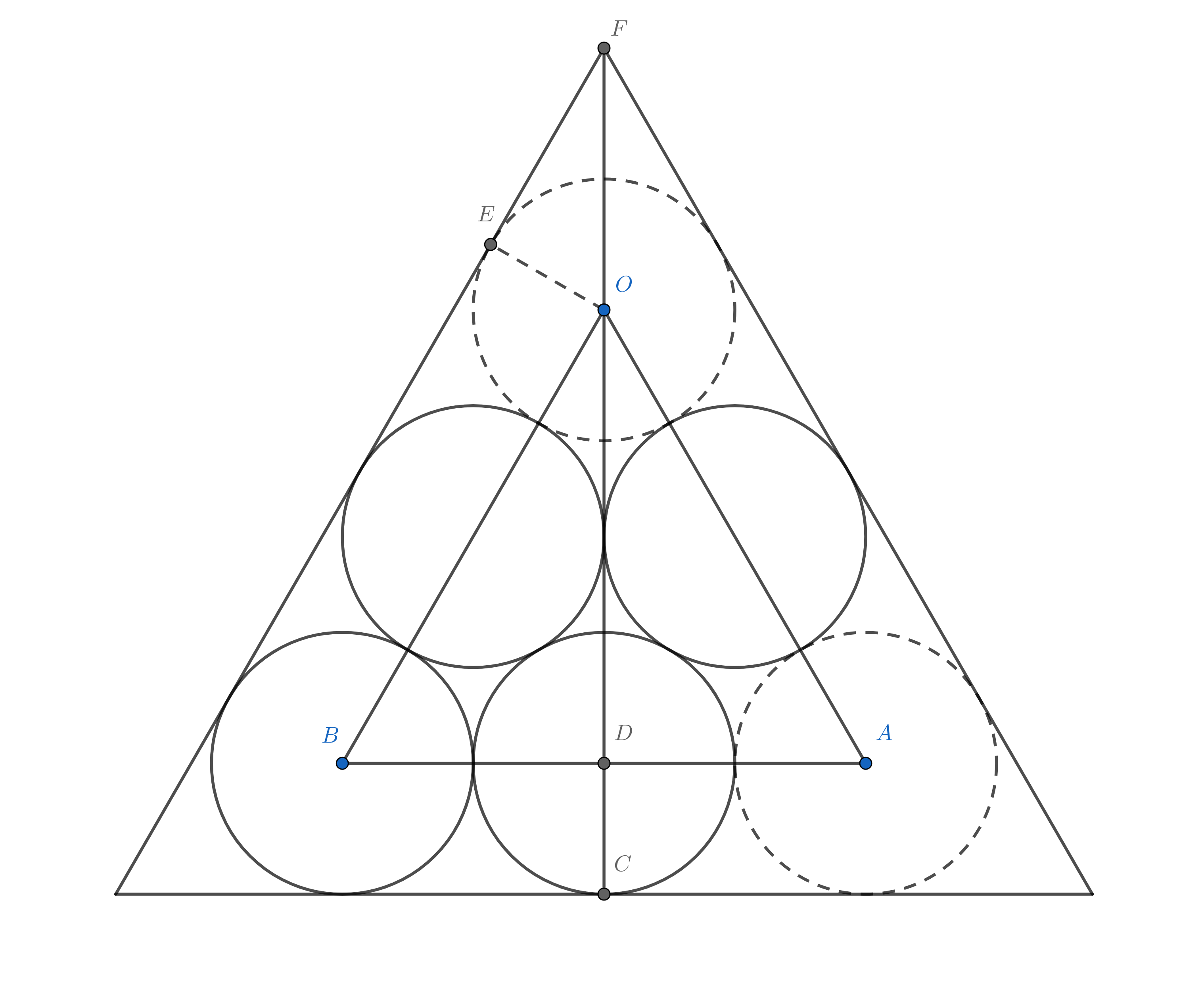
这时候直接代公式就可以了,$k=3$:
$$
\begin{aligned}
S&=\sqrt{3}k^2+(6-2\sqrt{3})k+4\sqrt{3}-6\\
&=9\sqrt{3}+18-6\sqrt{3}+4\sqrt{3}-6\\
&=12+7\sqrt{3}\\
&\approx24.124
\end{aligned}
$$
情况二
对于四个或五个圆,还有另一种面积较小的情况如图,切点$C$为$AB$中点。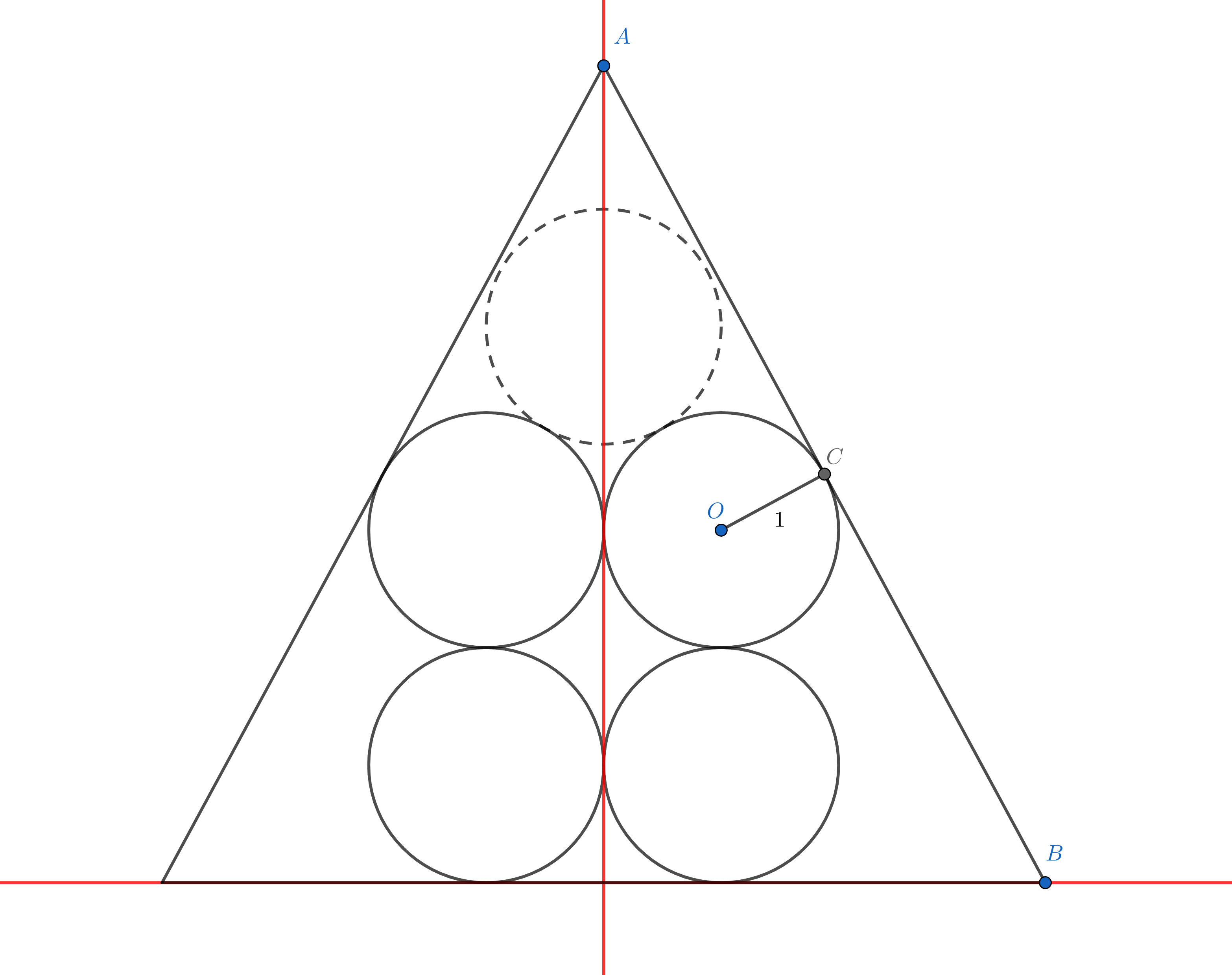
还是建系计算,思路与前述相同。
设$A(0,a)$,$B(b,0)$,可以列出方程:
$$
\begin{align*}
\frac{b}{a}+\frac{a^2-b^2}{2a}=3\\
(\frac{1}{2}b-1)^2+(\frac{1}{2}a-3)^2=1
\end{align*}
$$
根式解很复杂,所以就直接写近似结果了:$b\approx3.759$,$S\approx26.132>24.124$
情况一在空缺两位的情况下,空间利用率仍比情况二高,再一次展现了平面六角密堆积式的优越性。事实上,观察情况二的图可知情况一等价于下层两圆移至两边,可以在底不变甚至减小的情况下减小高,如此能够减小面积就不显奇怪了。
情况三
当然,情况一虽排列合理,但终究空缺两位,对于四个圆,很容易发现更小的外切三角形,即图中左下的直角三角形: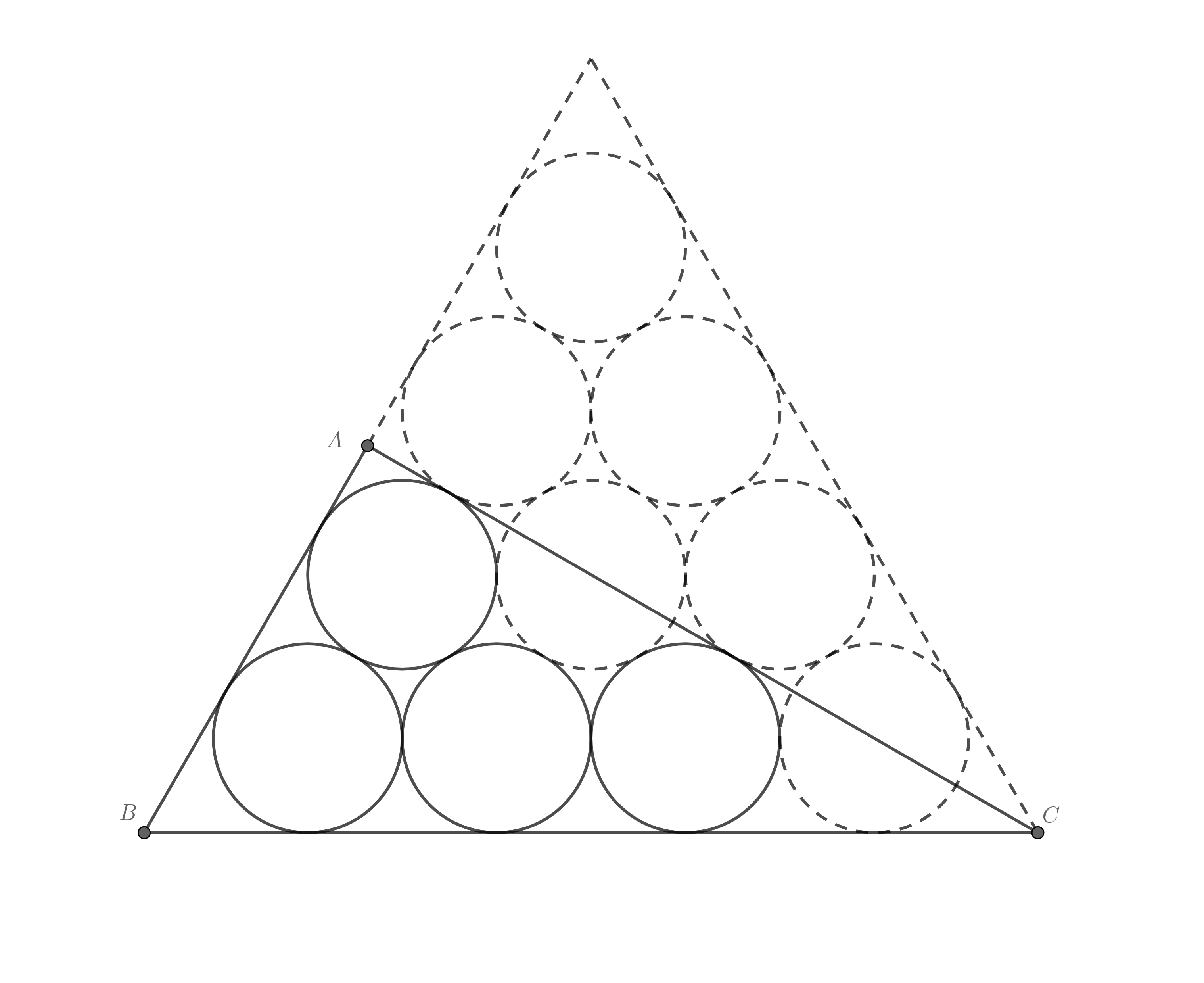
观察图形可只此直角三角形恰为10个圆的最小外切三角形的一半,于是可以用前述方法先求大等边三角形的面积,除以2即为直角三角形面积:
$$
\begin{aligned}
S&=(\sqrt{3}n^2+(6-2\sqrt{3})n+4\sqrt{3}-6)/2\\
&=(16\sqrt{3}+24-8\sqrt{3}+4\sqrt{3}-6)/2\\
&=9+6\sqrt{3}\\
&\approx19.392
\end{aligned}
$$
对于像4这样可以形成等边三角形的一半的数,不妨称其为半三角形数。半三角形数就是三角形数减去分割线通过的圆,再除以二。由此可以得到半三角形数的公式:
$$
a=\begin{cases}
n^2/4,\quad n\to \rm even\\
(n^2-1)/4,\quad n\to \rm odd
\end{cases}
$$
此时突然发现6也是半三角形数:$6=(5^2-1)/4$,于是作出6个圆的外切直角三角形: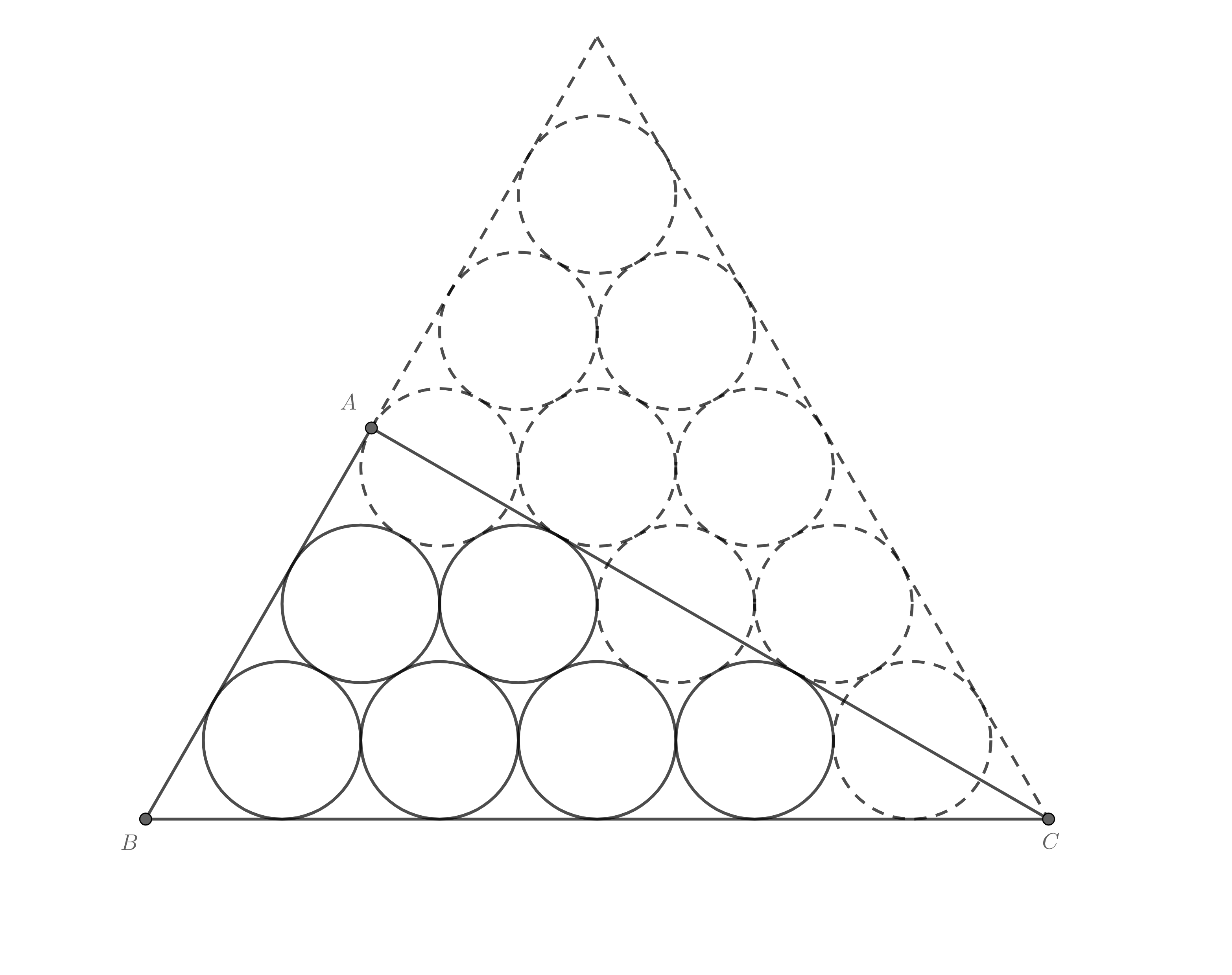
然后用和前面一样的方法计算面积:
$$
\begin{aligned}
S&=(\sqrt{3}n^2+(6-2\sqrt{3})n+4\sqrt{3}-6)/2\\
&=(25\sqrt{3}+30-10\sqrt{3}+4\sqrt{3}-6)/2\\
&=12+9.5\sqrt{3}\\
&\approx28.454
\end{aligned}
$$
明显比上面的情况一大。
同时是三角形数和半三角形数的情况不多见,可通过解方程$n^2/4=k(k+1)/2$或$(n^2-1)/4=k(k+1)/2$得到。
1000以下共有如下几组解($n$表示半三角形层数,$k$表示三角形层数,$c$表示对应圆的个数):
$$
\begin{align*}
n=2,k&=1,c=1\\
n=12,k&=8,c=36\\
n=70,k&=49,c=1225\\
n=408,k&=288,c=41616
\end{align*}
$$
或:
$$
\begin{align*}
n=5,k&=3,c=6\\
n=29,k&=20,c=210\\
n=169,k&=119,c=7140\\
n=985,k&=696,c=242556
\end{align*}
$$
除去相等的情况,三角形数和半三角形数分布很不均匀。两个三角形数之间的半三角形数分布不均,因此对于三角形数个圆,不能确定究竟是其排成的直角三角形,还是稍大于其的三角形数排成的等边三角形面积更小。
例如,4个圆排成的直角三角形面积小于6个圆排成的等边三角形,而9个圆排成的直角三角形面积(约39.249)大于10个圆排成的等边三角形(约38.785).
提出猜想3:在猜想2的基础上,对于上述半三角形数个圆(不等于某个三角形数),最小外切三角形可能为等边三角形的一半(带60°的直角三角形),面积为:
$$S=\frac{\sqrt{3}}{2}n^2+(3-\sqrt{3})n+2\sqrt{3}-3$$
也可能为稍大于其的三角形数排成的等边三角形,面积为:
$$S=\sqrt{3}k^2+(6-2\sqrt{3})k+4\sqrt{3}-6$$
不需要考虑其他的情况。
6. What about 100?
虽然没有得到一般的结论(甚至特殊的结论也没有证明),但对这个问题大致了解并提出猜想后,100个圆的情况也大致可以算出了。
100恰是半三角形数,于是根据猜想3,只需算100个圆排成的直角三角形面积和105个圆排成的等边三角形面积,分别为:
$$S_1=\frac{\sqrt{3}}{2}n^2+(3-\sqrt{3})n+2\sqrt{3}-3=57+182\sqrt{3}\approx372.233$$
$$S_2=\sqrt{3}k^2+(6-2\sqrt{3})k+4\sqrt{3}-6=78+172\sqrt{3}\approx375.913$$
大概就可以得到最小面积$S_1=57+182\sqrt{3}\approx372.233$。
7. 不等大的情况
不等大的情况比等大的复杂很多,关键在于圆与圆相切的方式更多样,需要考虑的情况多得多。需要注意的是不能太高估空隙的容纳能力,本来我以为大圆相切产生的空隙足够将小圆全部容纳其内,结果发现面积为100、99、98的三个圆相切产生的空隙仅能容纳面积大约为2.369的小圆,面积为100、99、98、97的四个圆相切产生的空隙也只能至多容纳面积大约为16.7的圆。
对于这个问题我还完全没有思路,还得留到以后解决。