群论学习笔记-4.循环群

直观理解

可以把循环群看作一个中心对称平面几何图形的旋转作用构成的群，例如旋转一个六叶风车，可以得到循环群$C_6$：

代数定义

若群$G$的每个元素都能表示为一个固定元素$a$的方幂，则$G$为由$a$生成的循环群，记作$\langle a\rangle$，$a$称为$\langle a\rangle$的一个生成元。

• 若$a$是无限阶元素，$\langle a\rangle=\{\cdots,a^{-3},a^{-2},a^{-1},e,a,a^2,a^3,\cdots\}$
• 若$a$是$n$阶元素，$\langle a\rangle=\{e,a,a^2,\cdots,a^{n-1}\}$，为$n$阶循环群($C_n$)

很容易看出，所有循环群都是交换群，所以循环群可由加法表示。例如，$C_6$可以表示为模6加法群$\langle\mathbb{Z}_6,+\rangle=\{0,1,2,3,4,5\}$，$\mathbb{Z}$上的加法群为无限循环群。

循环群的生成元不唯一：
设$\langle a\rangle$是$a$生成的循环群，设$a^l$也为生成元，则$a$可表示为$(a^l)^m=a^{lm}$

• 若$\langle a\rangle$是无限循环群，由于群的无限性，$lm=1$，易得$l=\pm1$，即无限循环群共有2个生成元：$a$和$a^{-1}$
• 若$\langle a\rangle$是$n$阶循环群，则$n\mid lm-1$，可得$l,n$互素；若$l,n$互素，那么存在整数$u,v$使$un+vl=1$，$a=(a^l)^{v}=a^{1-un}$，可得$a^l$也为生成元，即$a^l$为生成元的充要条件是$l,n$互素，所以$\langle a\rangle$共有$\phi(n)$个生成元

$\phi(n)$为欧拉函数，表示小于等于正整数$n$且与$n$互素的正整数的数目

循环群的子群

取$\langle a\rangle$中任意元素$a^k$可生成循环群$\langle a^k\rangle$。这样生成的$\langle a^k\rangle$是$\langle a\rangle$的子群，且$\langle a\rangle$的子群都可由这种方法生成。

从凯莱图来看，循环群子群的构造就是将原群中多个连续作用的箭头合并为一个箭头，来连接部分元素。例如$C_6$的子群：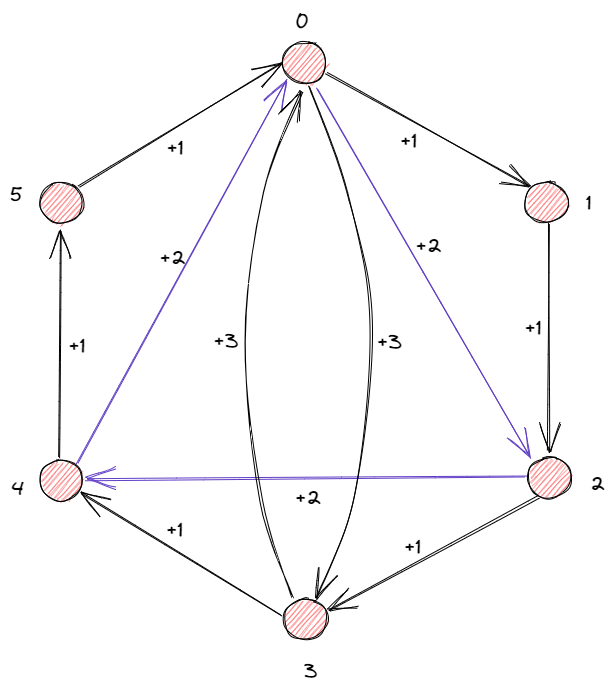

观察子群的阶数可知，有限循环群子群的阶数是其自身阶数的正因子，因而循环群子群的个数等于循环群阶数正因子的个数。而无限循环群的非单位子群都是无限循环群。

证明：设$H$是循环群$\langle a\rangle$的一个子群，若$H$是单位子群，则$H$显然是循环群，若$H$不是单位子群，设$a^m$是$H$中最小的$a$的正方幂，可证$H=\langle a^m\rangle$：
任取$H$中一个元素$a^l$，存在整数$q,r$满足$l=qm+r$，$0\le r<m$，于是：
$$a^l(a^{-m})^q=a^r\in H$$
由于$a^m$是最小的$a$的正方幂，$0\le r<m$，可知$r=0$，则$a^l=(a^m)^q$，所以$H=\langle a^m\rangle$，于是得证循环群的子群都为循环群。

因为无限循环群中的非单位元素都是无限阶元素，所以无限循环群的非单位子群也都是无限循环群。
对于$n$阶循环群$\langle a\rangle$及其子群$\langle a^m\rangle$，由上述证明很容易得到$m$能整除$n$，于是$a^m$的阶为$n/m$，$\langle a^m\rangle$的阶也为$n/m$。