群論學習筆記-4.循環群

直觀理解

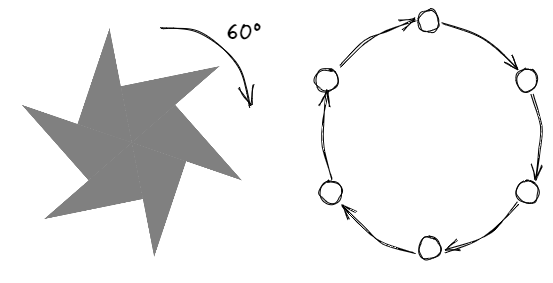
可以把循環群看作一個中心對稱平面幾何圖形的旋轉作用構成的群，例如旋轉一個六葉風車，可以得到循環群$C_6$：

代數定義

若群$G$的每個元素都能表示為一個固定元素$a$的方冪，則$G$為由$a$生成的循環群，記作$\langle a\rangle$，$a$稱為$\langle a\rangle$的一個生成元。

• 若$a$是無限階元素，$\langle a\rangle=\{\cdots,a^{-3},a^{-2},a^{-1},e,a,a^2,a^3,\cdots\}$
• 若$a$是$n$階元素，$\langle a\rangle=\{e,a,a^2,\cdots,a^{n-1}\}$，為$n$階循環群($C_n$)

很容易看出，所有循環群都是交換群，所以循環群可由加法表示。例如，$C_6$可以表示為模6加法群$\langle\mathbb{Z}_6,+\rangle=\{0,1,2,3,4,5\}$，$\mathbb{Z}$上的加法群為無限循環群。

循環群的生成元不唯一：
設$\langle a\rangle$是$a$生成的循環群，設$a^l$也為生成元，則$a$可表示為$(a^l)^m=a^{lm}$

• 若$\langle a\rangle$是無限循環群，由於群的無限性，$lm=1$，易得$l=\pm1$，即無限循環群共有2個生成元：$a$和$a^{-1}$
• 若$\langle a\rangle$是$n$階循環群，則$n\mid lm-1$，可得$l,n$互素；若$l,n$互素，那麼存在整數$u,v$使$un+vl=1$，$a=(a^l)^{v}=a^{1-un}$，可得$a^l$也為生成元，即$a^l$為生成元的充要條件是$l,n$互素，所以$\langle a\rangle$共有$\phi(n)$個生成元

$\phi(n)$為歐拉函數，表示小於等於正整數$n$且與$n$互素的正整數的數目

循環群的子群

取$\langle a\rangle$中任意元素$a^k$可生成循環群$\langle a^k\rangle$。這樣生成的$\langle a^k\rangle$是$\langle a\rangle$的子群，且$\langle a\rangle$的子群都可由這種方法生成。

從凱萊圖來看，循環群子群的構造就是將原群中多個連續作用的箭頭合並為一個箭頭，來連接部分元素。例如$C_6$的子群：

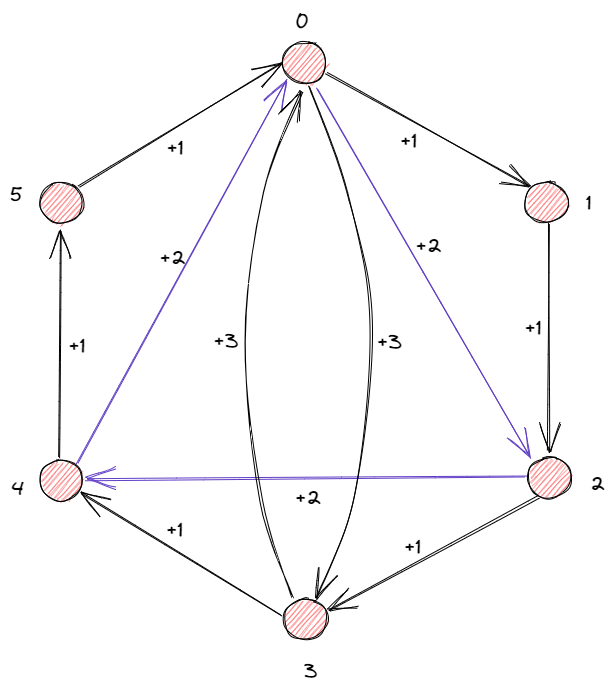
觀察子群的階數可知，有限循環群子群的階數是其自身階數的正因子，因而循環群子群的個數等於循環群階數正因子的個數。而無限循環群的非單位子群都是無限循環群。

證明：設$H$是循環群$\langle a\rangle$的一個子群，若$H$是單位子群，則$H$顯然是循環群，若$H$不是單位子群，設$a^m$是$H$中最小的$a$的正方冪，可證$H=\langle a^m\rangle$：
任取$H$中一個元素$a^l$，存在整數$q,r$滿足$l=qm+r$，$0\le r<m$，於是：
$$a^l(a^{-m})^q=a^r\in H$$
由於$a^m$是最小的$a$的正方冪，$0\le r<m$，可知$r=0$，則$a^l=(a^m)^q$，所以$H=\langle a^m\rangle$，於是得證循環群的子群都為循環群。

因為無限循環群中的非單位元素都是無限階元素，所以無限循環群的非單位子群也都是無限循環群。
對於$n$階循環群$\langle a\rangle$及其子群$\langle a^m\rangle$，由上述證明很容易得到$m$能整除$n$，於是$a^m$的階為$n/m$，$\langle a^m\rangle$的階也為$n/m$。