群论学习笔记-2.置换群

置换与对称群

置换

设$\Omega$是由$n$个文字组成的集合: $\Omega=\{\alpha_1,\alpha_2,\cdots,\alpha_n\}$
$\Omega$到自身的一个一一映射称为$\Omega$上的一个$n$元置换。
设$\sigma$是$\Omega=\{\alpha_1,\alpha_2,\cdots,\alpha_n\}$上的一个置换，用$\alpha_i^{\sigma}\quad(i=1,2,\cdots,n)$表示，则$\sigma$表成：
$$\sigma=\begin{pmatrix}\alpha_1,\alpha_2,\cdots,\alpha_n\\ \alpha_1^{\sigma},\alpha_2^{\sigma},\cdots,\alpha_n^{\sigma}\end{pmatrix}$$

对称群

$n$个元素具有$n!$种不同的排列，因此对其有$n!$个$n$元置换，用$S_n$表示这$n!$个置换的集合。
定义$S_n$上置换的乘法为两个置换的连续作用，例如：
$$\begin{pmatrix}1,2,3,4\\2,4,1,3\end{pmatrix}\cdot\begin{pmatrix}1,2,3,4\\2,1,4,3\end{pmatrix}=\begin{pmatrix}1,2,3,4\\1,3,2,4\end{pmatrix}$$
$S_n$上的置换乘法具有如下性质：

• 满足结合律: $(\sigma\tau)\rho=\sigma(\tau\rho)\quad(\sigma,\tau,\rho\in S_n)$
• 存在单位元: $e=\begin{pmatrix}1,2,\cdots,n\\1,2,\cdots,n\end{pmatrix}$
• 每个$n$元置换在$S_n$中存在逆元

显然，$S_n$对置换乘法构成群，称为$n$元对称群，$S_2$是2阶交换群，但当$n\ge3$时，$S_n$不是交换群。

置换的轮换表法

若置换$\sigma$作用于$n$个元素中的$\alpha_1,\alpha_2,\cdots,\alpha_m$，使：
$$\alpha_1^\sigma=\alpha_2,\quad \alpha_2^\sigma=\alpha_3,\quad\cdots,\quad \alpha_m^\sigma=\alpha_1$$
且其余$n-m$个元素不变，则称$\sigma$为一个$m$-轮换，简称轮换，记作：
$$\sigma=(\alpha_1,\alpha_2,\cdots,\alpha_m)$$
$m$称为轮换的长度，当$m=1$时，$\sigma$是恒等置换；当$m=2$时，$\sigma$称为一个对换。
若$\alpha_1,\alpha_2,\cdots,\alpha_m$与$\beta_1,\beta_2,\cdots,\beta_l$，
则两个置换$\sigma=(\alpha_1,\alpha_2,\cdots,\alpha_m)$和$\tau=(\beta_1,\beta_2,\cdots,\beta_l)$称为不相交的，很容易看出，不相交的轮换可交换。

定理：任何有限置换都可以表示为一些不相交的轮换的乘积，且表法唯一。例如：
$$\begin{pmatrix}1,2,3,4,5,6,7,8\\3,1,5,4,2,8,7,6\end{pmatrix}=(1,3,5,2)(4)(6,8)(7)=(1,3,5,2)(6,8)$$
问题分析：由于轮换是不相交的，那么它们互不影响，根据轮换的性质，易得$m$-轮换$\sigma^l=\sigma^{l+m}$，即重复此轮换$m$次后会还原为初始状态，而有限置换在重复多次后也必然部分地还原为初始状态，则在某次重复时还原的元素就确定了一个轮换，由此入手即可证明。
证明：设$\sigma$是$1,2,\cdots,n$的一个置换，任取$1,2,\cdots,n$中的一个设为$\alpha$，作序列：
$$\alpha=\alpha^{\sigma^0},\alpha^{\sigma^1},\alpha^{\sigma^2},\cdots$$
因为$\alpha^{\sigma^k}\in\{1,2,\cdots,n\}$，所以序列一定包含重复的文字，设$\alpha^{\sigma^m}$是第一个在前面出现过的文字，且$\alpha^{\sigma^m}=\alpha^{\sigma^i}$ ($0\le i<m$)，那么$\alpha,\alpha^{\sigma},\cdots,\alpha^{\sigma^{m-1}}$各不相同。
若$i\not=0$，则$(\alpha^{\sigma^{m-1}})^{\sigma}=(\alpha^{\sigma^{i-1}})^{\sigma}$，产生矛盾，因此$i=0$，所以$\alpha^{\sigma^m}=\alpha$，作轮换：
$$\sigma_1=(\alpha,\alpha^{\sigma},\cdots,\alpha^{\sigma^{m-1}})$$
则$\sigma$与$\sigma_1$在$\alpha,\alpha^{\sigma},\cdots,\alpha^{\sigma^{m-1}}$作用相同。
若$m=n$，则$\sigma=\sigma_1$是一个轮换；若$m<n$，则在剩余文字中选取$\beta$重复上述过程，得到轮换：
$$\sigma_2=(\beta,\beta^{\sigma},\cdots,\beta^{\sigma^{r-1}})$$
由于$\sigma$是一一映射，$\sigma_1$与$\sigma_2$不相交。继续此过程即可得到$\sigma$的轮换表法。
表法唯一性是很明显的。
推论：若$\sigma=\sigma_1\sigma_2\cdots\sigma_s$，其中$\sigma_i$的长度为$l_i$ ($l=1,2,\cdots,s$)，则$\sigma$的阶数等于$l_1,l_2,\cdots,l_s$的最小公倍数$[l_1,l_2,\cdots,l_s]$，这是很明显的。

置换的奇偶性 交错群

置换的奇偶性

每个轮换都可表成一些对换的乘积：
$$(a_1,a_2,\cdots,a_m)=(a_1,a_2)(a_1,a_3)\cdots(a_1,a_m)$$
因此每个置换都可表成一些对换的乘积，但表法不唯一，例如：
$$\begin{pmatrix}1,2,3,4,5\\2,3,1,5,4\end{pmatrix}=(1,2)(1,3)(4,5)=(2,3)(1,2)(4,5)=(2,3)(1,2)(1,3)(4,5)(1,3)$$

定理：$n$元置换$\sigma$表成对换的乘积后，乘积中对换个数的奇偶性由$\sigma$唯一确定，且与$n$元排列$1^{\sigma},2^{\sigma},\cdots,n^{\sigma}$的奇偶一致。

逆序数：规定标准排序由小到大，若排列中某两个元素排列的次序与标准次序不同，就称这两个数构成一个逆序，一个排列中所有逆序的总和称为这个排列的逆序数，记作$N(p_1,p_2,\cdots,p_n)$，如$N(1,2,3,4)=0$，$N(1,2,4,3)=1$

排列的奇偶性：逆序数为奇数的排列是奇排列，反之为偶排列。

证明：设$\sigma=\sigma_1\sigma_2\cdots\sigma_m$，即将$m$次对换作用于$1,2,\cdots,n$上。对换改变数列的奇偶，$m$次对换就将奇偶改变$m$次，由于$1,2,\cdots,n$是一个偶排列，所以$m$的奇偶性与$1^{\sigma},2^{\sigma},\cdots,n^{\sigma}$一致。

交错群

若$n$元置换$\sigma$可以表成奇数个对换的乘积，则称$\sigma$为奇置换，反之则为偶置换。
从定义可知，在$n!$个$n$元置换中，奇偶置换个数相同，都为$n!/2$个。恒等置换是偶置换，两个偶置换之奇为偶置换，偶置换的逆置换也是偶置换。

于是，$n$元偶置换对置换的乘法构成一个群，其阶为$n!/2$，称为$n$元交错群，记作$A_n$

选取对称群$S_n$中每个元素取其平方，所得平方元恰好是对称群的一半，且构成对应的交错群，例如从$S_3$构造$A_3$：

原始元素	平方元素
$e$	$e$
$(1,2)$	$e$
$(2,3)$	$e$
$(1,3)$	$e$
$(1,2,3)$	$(1,2)(2,3)$
$(1,2)(2,3)$	$(1,2,3)$

这样做的原理在于对称群中原始置换平方后全部转化为偶置换，消除了所有奇置换，满足交错群的条件。

置换群

定义

由$n$元置换组成的群称为$n$元置换群，例如$n$元对称群和$n$元交错群都是$n$元置换，显然$n$元置换群都为$n$元对称群的子群。
一个置换实际变动的文字个数称为这个置换的次数，而一个置换群实际变动的文字个数称为这个群的次数，例如$(1,2,3)$是一个3次置换，$G=\{e,(1,2,3),(1,3,2)\}$是一个3次置换群。

凯莱图

置换群的凯莱图可以表示为凸多面体，称为置换多面体，其中一些置换群的凯莱图对应于正多面体。
$A_4$的凯莱图对应于正四面体：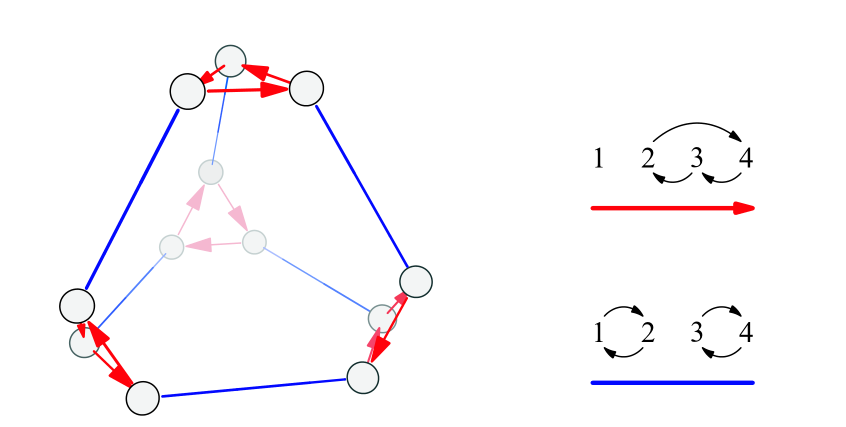

$S_4$的凯莱图对应于正六面体或正八面体：

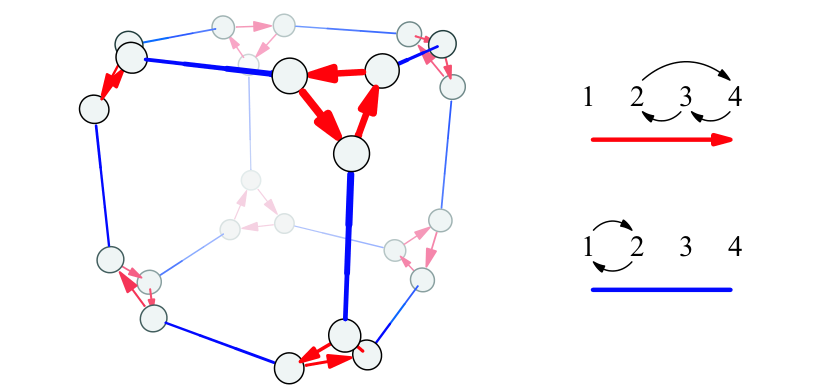
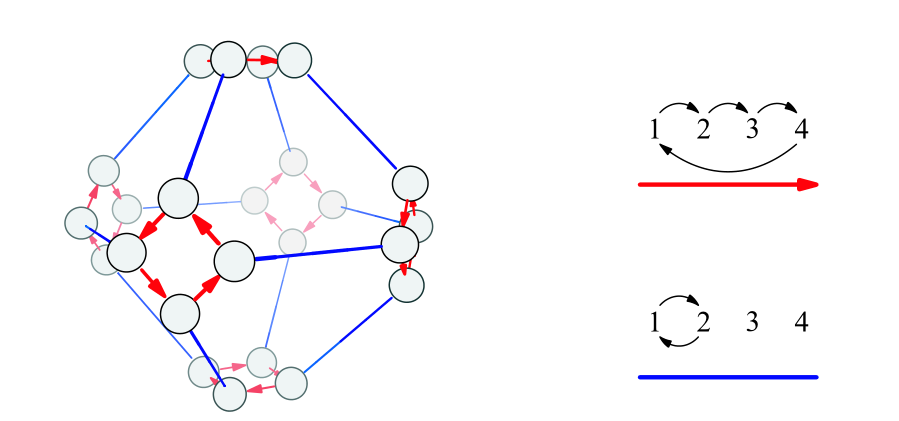
$A_5$的凯莱图对应于正十二面体或正二十面体：

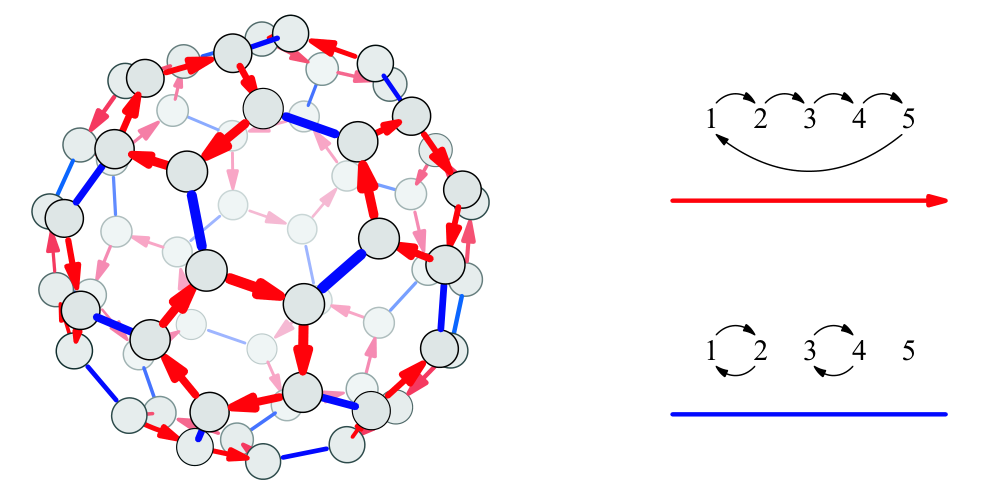
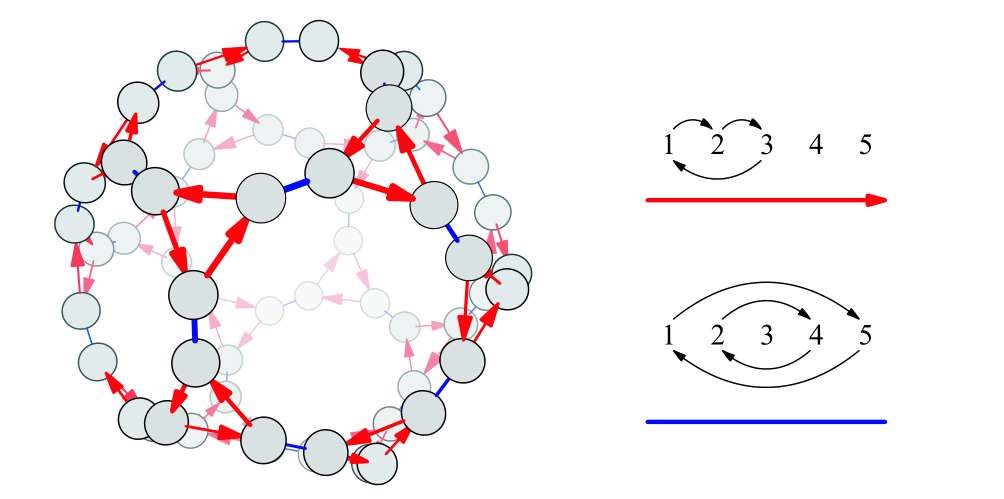
由于三维空间中正多面体只有五种，更高阶的一些置换群的凯莱图对应于高维正多面体。

可以看到$S_4$和$A_5$对应的正多面体不唯一，由欧拉示性数定理可知正多面体满足：
$$(\frac{2}{m}+\frac{2}{n}-1)E=2$$
其中$m$表示一个面的边数或顶点数，$n$表示每个顶点关联的棱数，$E$表示总棱数，于是：

• $m=4,n=3,E=12$，对应正六面体
• $m=3,n=4,E=12$，对应正八面体
• $m=5,n=3,E=30$，对应正十二面体
• $m=3,n=5,E=30$，对应正二十面体

可以看到正六面体和正八面体的$m,n$相反，$E$相同，正十二面体和正二十面体也有相同的关系。则这样一对多面体互为对偶多面体。这其实意味着群的同构，在此不多叙述。