群论学习笔记-1.群的概念
群是代数的结构,也是数学中最早被认识和研究的结构,并且这个“群”的结构在“在十九世纪逐步征服了数学这门科学”。(皮亚杰《结构主义》)
本学习笔记记录我自学群论(主要是有限群论)的一些思考与总结。
主要参考内森·卡特《群论彩图版》和王萼芳《有限群论基础》
直观理解
一言以蔽之,群论是研究对称(Symmetry)的理论,但究竟什么是”对称”?
翻转开关
现在我们有两个开关,每个开关有开合两种状态。可以看到这两个开关的组合共有4种状态,对其有2种基本操作,即”翻转开关1”和”翻转开关2”,每一种状态都可由基本操作的组合得到。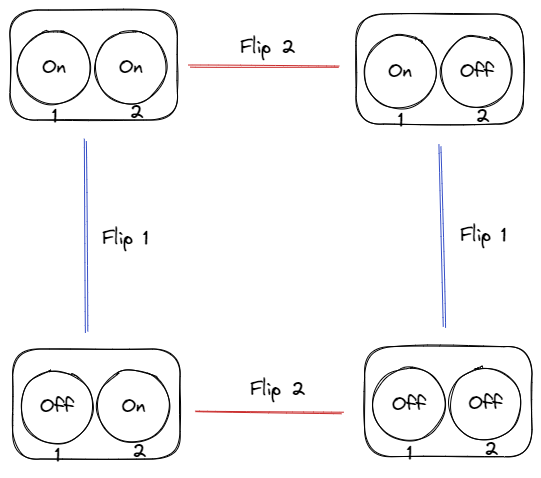
翻转长方形
一张长方形纸片,对其进行“竖直翻转”和“水平翻转”操作: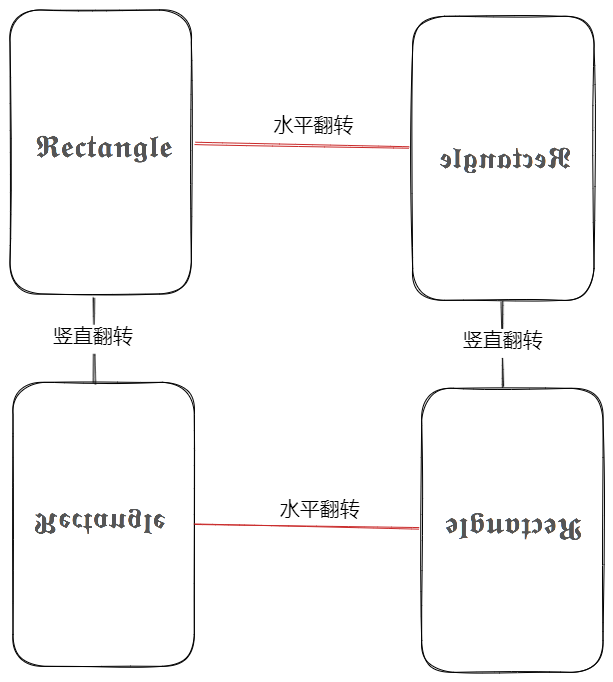
可以看到这种操作与翻转开关很相似,每次操作将对象变换为另一种状态,但其在某种意义上不变。
对称与群
上面的两种操作可抽象为等价的作用,两种操作表示同一个群。这些作用(Action)即为对称(Symmetry),而这些作用的集合就是一个群。
事实上,对称(Symmetry)就是对某个数学对象的(可逆)变换,可以理解为映射$\phi : X\to X$ ($X$映射到本身意味着这个对象本身是不变的)。因而,群的研究对象可以看作对称,也可以看作一种作用。
一些给定的作用的系统或集合就是一个群,这些作用满足如下性质:
- 每个作用都是可逆的
- 每个作用都是确定性的
- 任何连续作用的序列仍是一个作用
- “什么也不做”也是一个作用
一个群可以看作作用的集合,也可看作定义了某种作用的状态的集合。
最基本的作用称为生成元(Generators),生成元的集合为生成集合,一般表示为$S$,$S$是最小的使群中所有元素都可表示为$S$中元素乘积的子集(子群)。
特别地,若群中任意两个连续作用交换后结果相同,此群为交换群(阿贝尔群)。
凯莱图
凯莱图(Cayley graph)是群的可视化工具,将上面的作用图简化,即可得到这个群的凯莱图: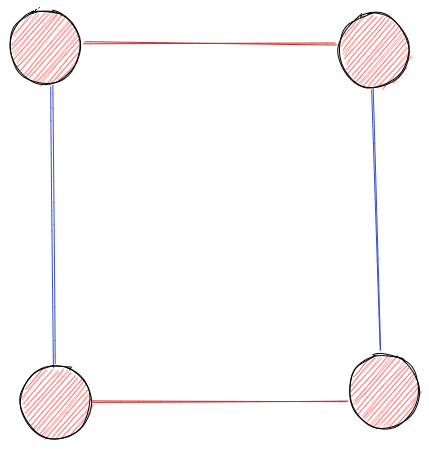
这个群就是Klein四元群$V_4$
图中不同颜色的边表示不同生成元,若某生成元$s=s^{-1}$,该生成元用无向边表示,否则用有向箭头表示。
由群作用的性质,可以得到凯莱图主要的一些性质:
- 连通性(Connectedness):图是连通的
- 同质性(Homogeneity):对任意顶点对$x,y$,仅有一种着色图同构将$x$映射到$y$
这点是说,任何图论陈述从$x$顶点出发为真,则从$y$顶点出发亦为真,保证了群作用关系的一致性(例如在$S_3$中,任意顶点出发$f\cdot r\cdot f=r^{-1}$恒成立) - 正则性(Regularity):对任意颜色$s\in S$($S$即生成集合),有一条$s$-边指向顶点$x$,一条$s$-边从顶点$x$发出,若$S$中有$k$个元素,则每个顶点都有$k$条边指入,$k$条边指出
(From Cayley graphs and the geometry of groups by Terence Tao)
代数定义
定义
设$G$是一个非空集合, 在$G$中定义了一种代数运算, 称为“乘法”,记作“$\cdot$”.
若$G$对这种运算满足如下条件:
- 封闭性:$\forall a,b\in G,a\cdot b\in G$
- 结合律:$(a\cdot b)\cdot c=a\cdot (b\cdot c)$
- 单位元的存在:存在$e$使$e\cdot a=a\cdot e=a$
- 逆元的存在:对任意$a$, 存在$a^{-1}$使$a^{-1}\cdot a=a\cdot a^{-1}=e$
则$G$称为一个群。
若群$G$还满足交换律,那么$G$就称作一个交换群或阿贝尔群,交换群的运算可用加法表示,记作“+”.
此时,该运算满足:
- 封闭性:$\forall a,b\in G,a+b\in G$
- 结合律:$(a+b)+c=a+(b+c)$
- 零元素的存在:存在元素$0$使$0+a=a+0=a$
- 负元素的存在:对任意$a$, 存在$-a$使$(-a)+a=a+(-a)=0$
- 交换律:对任意两个元素$a,b$, $a+b=b+a$
简单性质
- 单位元唯一
- 每个元素只有一个逆元素, $(a^{-1})^{-1}=a$
- 消去律成立:若$ab=ac$, 则$b=c$; 若$ba=ca$, 则$b=c$
- 指数律成立:$a^m\cdot a^n=a^{m+n},(a^m)^n=a^{mn}\quad(m,n\in \mathbb{Z})$
- 若$ab=ba,(ab)^n=a^nb^n\quad(n\in\mathbb{Z})$
- 对任意元素$a,b$, $ax=b$有唯一解
群的阶
如果群$G$包含的元素个数有限,则称$G$为有限群,否则称$G$为无限群。
例如,Klein四元群是有限群,$\mathbb{Z}$上的加法群是无限群。
有限群$G$所包含的元素个数称为$G$的阶,记作$|G|$。设$a$是$G$中一个元素,若存在正整数$k$使$a^k=e$,则$a$为有限阶元素,满足$a^k=e$的最小正整数$k$为$a$的阶。单位元是唯一的1阶元素,有限群的所有元素都为有限阶元素。
例如,Klein四元群是4阶群(阶数最小的非循环群),除单位元外所有元素都是2阶的。
若$a$是$G$的$k$阶元素,$a^l=a^m\to k\mid l-m$
若$a$是$G$的无限阶元素,$a^l=a^m\to l=m$