OpAEOLUS-2.數學模型

分析已有研究對紙飛機的數學建模，以及吐槽

1. 簡單受力分析

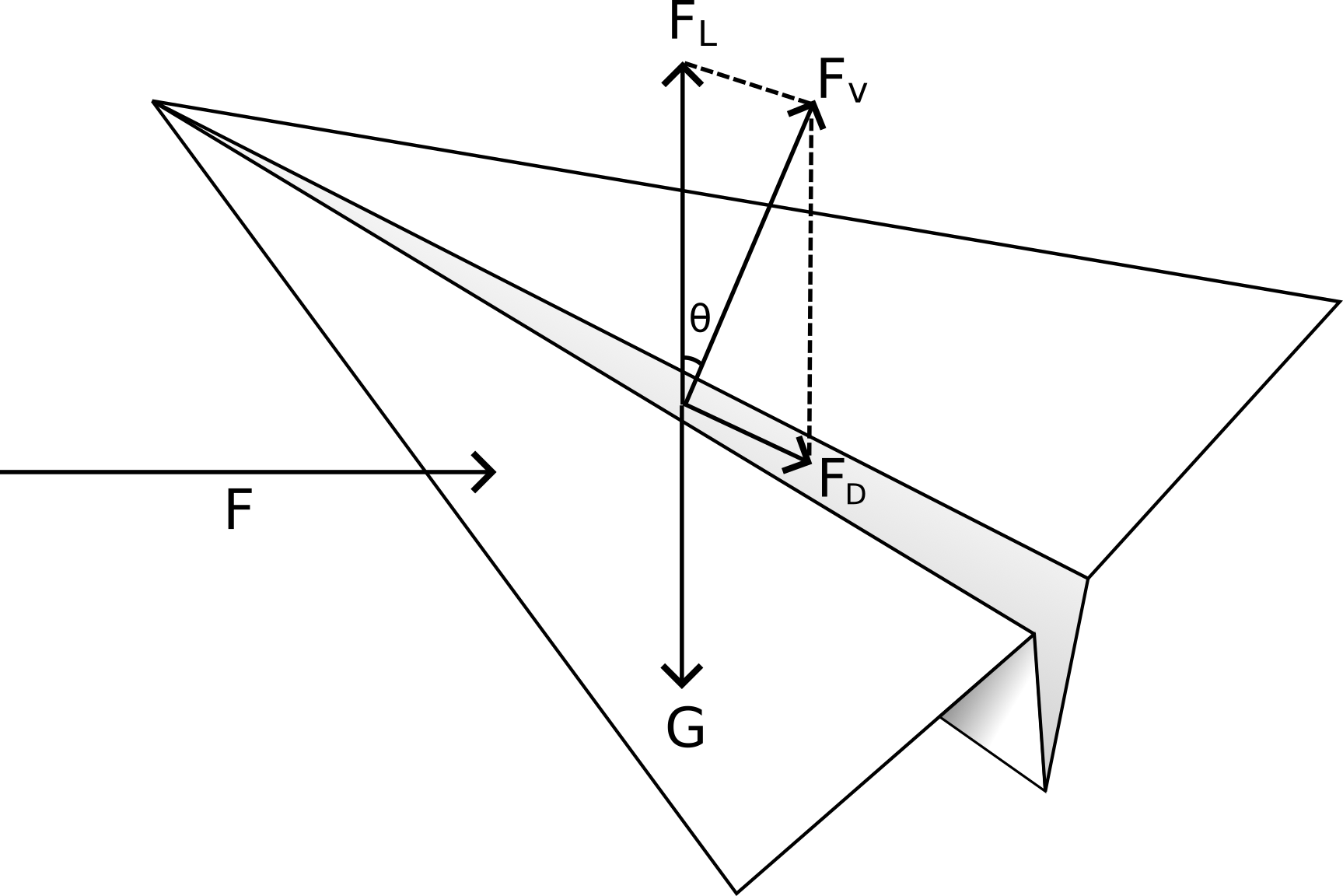
如圖, 可得^[1][2]:
$$F_v=F\sin\theta$$
$$F_L=F_v\cos\theta=F\sin\theta\cdot\cos\theta=\frac{1}{2}F\sin2\theta$$
$$F_D=F_v\sin\theta=F\sin\theta\cdot\sin\theta=F\sin^2\theta$$
可知當$\theta=45°$時$F_L$取到最大值，有文獻直接由此得出拋射角為45°最佳，實則不可，紙飛機方向時刻發生變化，而這種分析僅針對瞬時，只能作為簡單參考。

2. 簡單軌跡方程

對紙飛機豎直平面中位置分析, 可得^[3]:
$$
\begin{cases}
x(t)=vt\cdot\cos\theta\\
y(t)=vt\cdot\sin\theta-\frac{gt^2}{2}
\end{cases}
$$
可得紙飛機軌跡方程為:
$$y=x\cdot\tan\theta-\frac{x^2g}{2v^2\cos^2\theta}$$
求導得:
$$y’=\tan\theta-\frac{xg}{v^2\cos^2\theta}$$
當$v’=0$時, $x=\frac{v^2}{2g}\sin^2\theta$, 當$\theta=45°$時, $x_{max}=\frac{v^2}{2g}$, 由此得最佳拋射角為45°.

這樣的推導邏輯上沒有問題，但考慮因素太少，把紙飛機飛行理想化為簡單拋體運動，結果誤差極大。對於紙飛機這種質量、初速度小的飛行體，考慮空氣升阻力是必要的。

3. 較復雜的數學模型

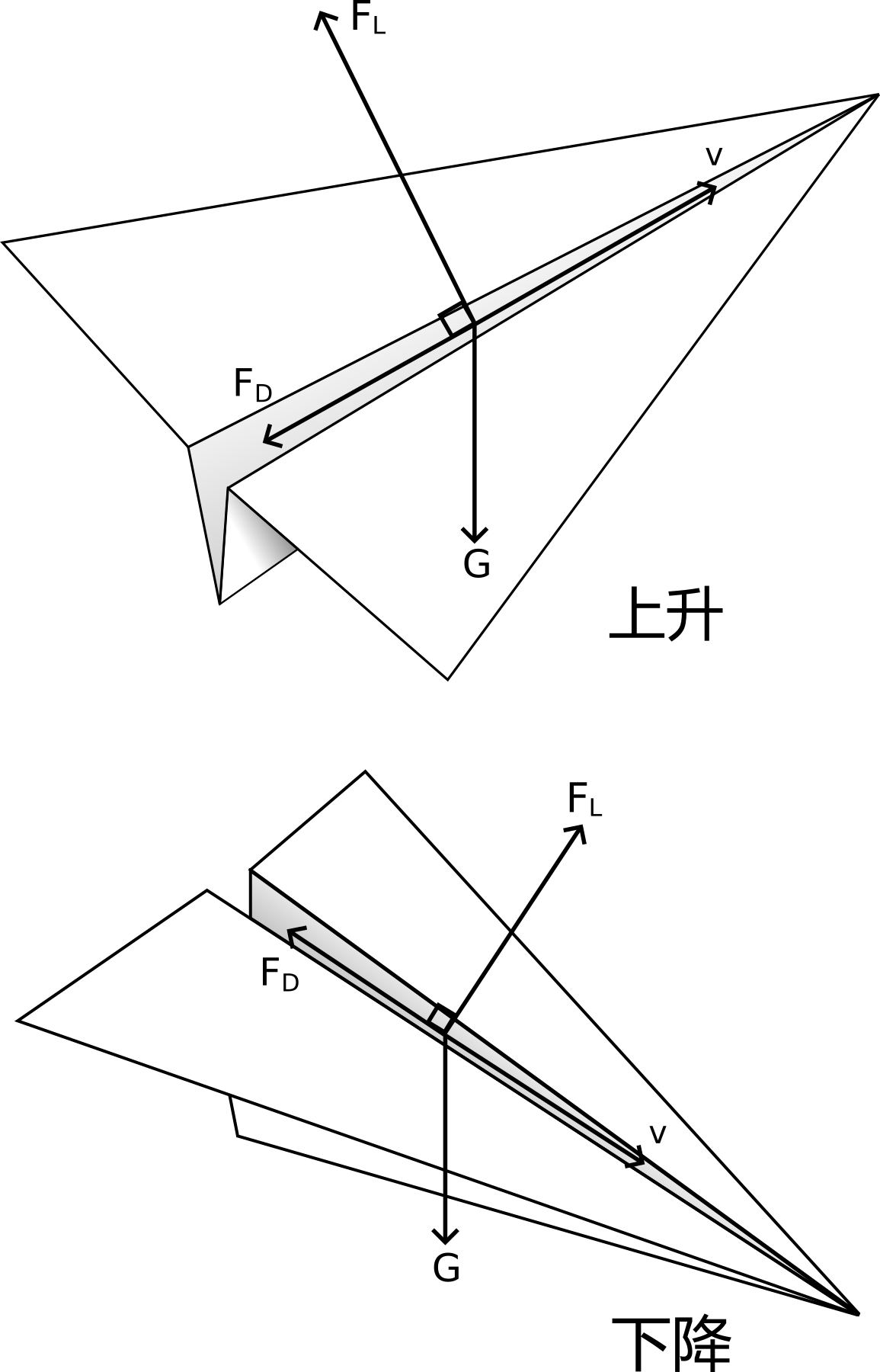
上升階段y方向:
$$G+F_D\cdot\sin\theta-F_L\cdot\cos\theta=ma_{1y}$$
$$v_{0y}=v_0\cdot\sin\theta$$
$$v_{1y}=v_{0y}-\int_{0}^{t_1} a_{1y}\cdot tdt$$
$$h=h_0+\int_{0}^{t_1} v_{1y}\cdot tdt$$
下降階段y方向:
$$G-F_D\cdot\sin\beta-F_L\cdot\cos\beta=ma_{2y}$$
$$v_{2y}=\int_{0}^{t_2} a_{2y}\cdot tdt$$
$$h=\int_{0}^{t_2} v_{2y}\cdot tdt$$
上升階段x方向:
$$F_D\cdot\cos\theta+F_L\cdot\sin\theta=ma_{1x}$$
$$v_{0x}=v_0\cdot\cos\theta$$
$$v_{1x}=v_{0x}-\int_{0}^{t_1} a_{1x}\cdot tdt$$
$$s_1=\int_{0}^{t_1} v_{1x}\cdot tdt$$
下降階段x方向:
$$F_L\cdot\sin\beta-F_D\cdot\cos\beta=ma_{2x}$$
$$v_{2x}=\int_{0}^{t_2} a_{2x}\cdot tdt$$
$$s_2=\int_{0}^{t_2} v_{2x}\cdot tdt$$
最終得到$s=s_1+s_2$. ^[1] (部分過程有修改)
同時，分析過程可得軌跡大約是: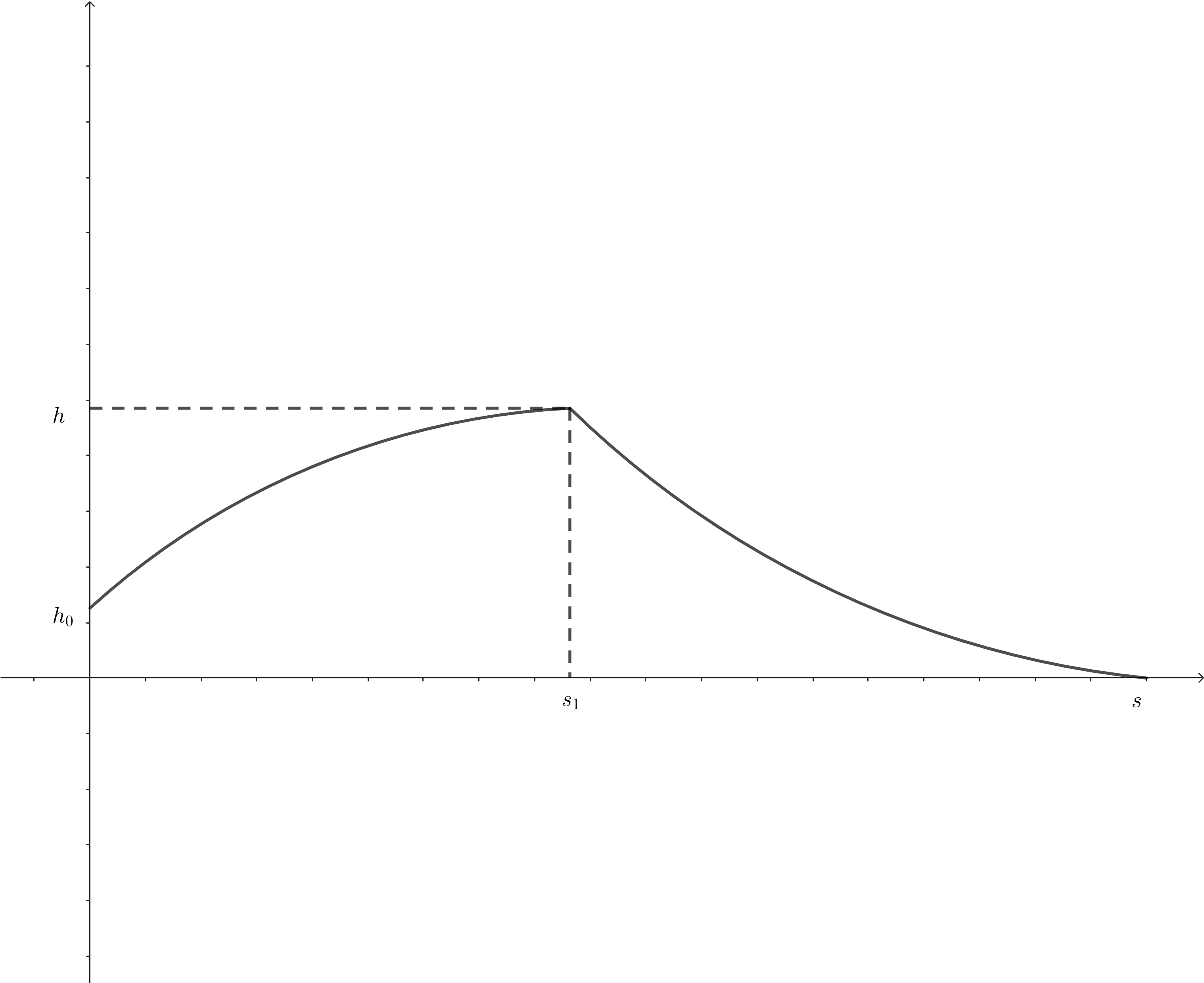

與現實情況基本符合

此模型考慮因素較多，同時也較好理解，但未知變量多，且多次積分，難以計算。本次研究將主要參考此模型進行修改，得出更好的數學模型。

4. 更復雜的數學模型

這是關注留空時間的數學模型^[4]，然而我看不懂。
只能盡可能理解一下

對於初速度:
$$v_x=v\cdot\cos\alpha,\quad v_y=v\cdot\sin\alpha$$
設上升到最大高度過程中水平與豎直方向分速度分別為$v_{x2},v_{y2}$, 則這一過程中水平與豎直方向分速度分別為:
$$\int(v_{x2}-v_0\cos\alpha)dt,\quad\int(v_{y2}-v_0\sin\alpha)dt$$
對於升力有:
$$F_L=C_L\cdot\frac{1}{2}\rho V^2S=[C_{L0}+\frac{\partial C_L}{\partial\alpha}\alpha]\frac{1}{2}\rho V^2S$$
對於阻力有:
$$F_D=C_D\cdot\frac{1}{2}\rho V^2S=[C_{D0}+\varepsilon C_L^2]\frac{1}{2}\rho V^2S$$
(偏微分+流體力學, 已經超越我的理解極限了)
得到推進力方程:
$$
\begin{cases}
F_x=(C_T\cos\theta+C_x)\frac{1}{2}\rho(V_x^2+V_z^2)S\\
F_z=(-C_T\sin\theta+C_z)\frac{1}{2}\rho(V_x^2+V_z^2)S+mg_0
\end{cases}
$$
(/ﾟДﾟ)/ $C_T$是什麼???
如果四種力相互抵消，留空時間會更長:
$$\dot{s_1}=\dot h=v_0\cdot\sin\alpha,\quad\dot{s_2}=\dot l=v_0\cdot\cos\alpha$$
因此:
$$
\begin{bmatrix} \dot{s_1}\\ \dot{s_2} \end{bmatrix}
=\begin{bmatrix} \dot{h}\\ \dot{l} \end{bmatrix}
=\begin{bmatrix} v_0\cdot\sin\alpha\\v_0\cdot\cos\alpha \end{bmatrix}
$$
(/ﾟДﾟ)/ (/ﾟДﾟ)/ 好吧我放棄了(滾去補數學基礎)

5. 總結

談一談看了這些論文的感想。
這些論文都出自不很正規的刊物，看完可以感覺到內容水的成分比較多。出現了扯不相關內容湊字數，給出公式但全程沒有用的情況。
看來這些論文都只能作為簡單參考，具體問題還要自己分析。

6. 參考

[1]尚余祥. 利用理論力學知識對紙飛機飛行距離的研究[J]. 科技風, 2019, 7: 225-227
[2]高吉, 賈文太. 紙飛機投擲的數學模型[J]. 科技風, 2019, 9: 77
[3]董曉紅, 康平. 紙飛機的飛行原理數學建模[J]. 科技風, 2019, 11: 83
[4]王微, 趙明程. 基於重心與投擲角度對紙飛機留空時間影響的分析[J]. 菏澤學院學報, 2022, 10: 10-12