记一道三角函数题

Posted on In
记一道离谱的题目，以及推出的一些结论

1. 题目

设三个角$A\not=B\not=C$，满足:
$$\cos A+\cos B+\cos C=0,\quad\sin A+\sin B+\sin C=0$$
求证$\cos^2A+\cos^2B+\cos^2C=\frac{3}{2}$.

2. 简化情况

令$C=-\frac{1}{2}\pi$, 则$\cos A+\cos B=0$,
又由$\sin C=-1,\sin A+\sin B+\sin C=0$得$\sin A=\sin B=\frac{1}{2}$, 即$A=\frac{1}{6}\pi,B=\frac{5}{6}\pi$.
易得$\cos^2A+\cos^2B+\cos^2C=\frac{3}{2}$.

3. 猜想

满足条件的一组$A,B,C$的终边三等分单位圆.

4. 证明

充分性的几何证明

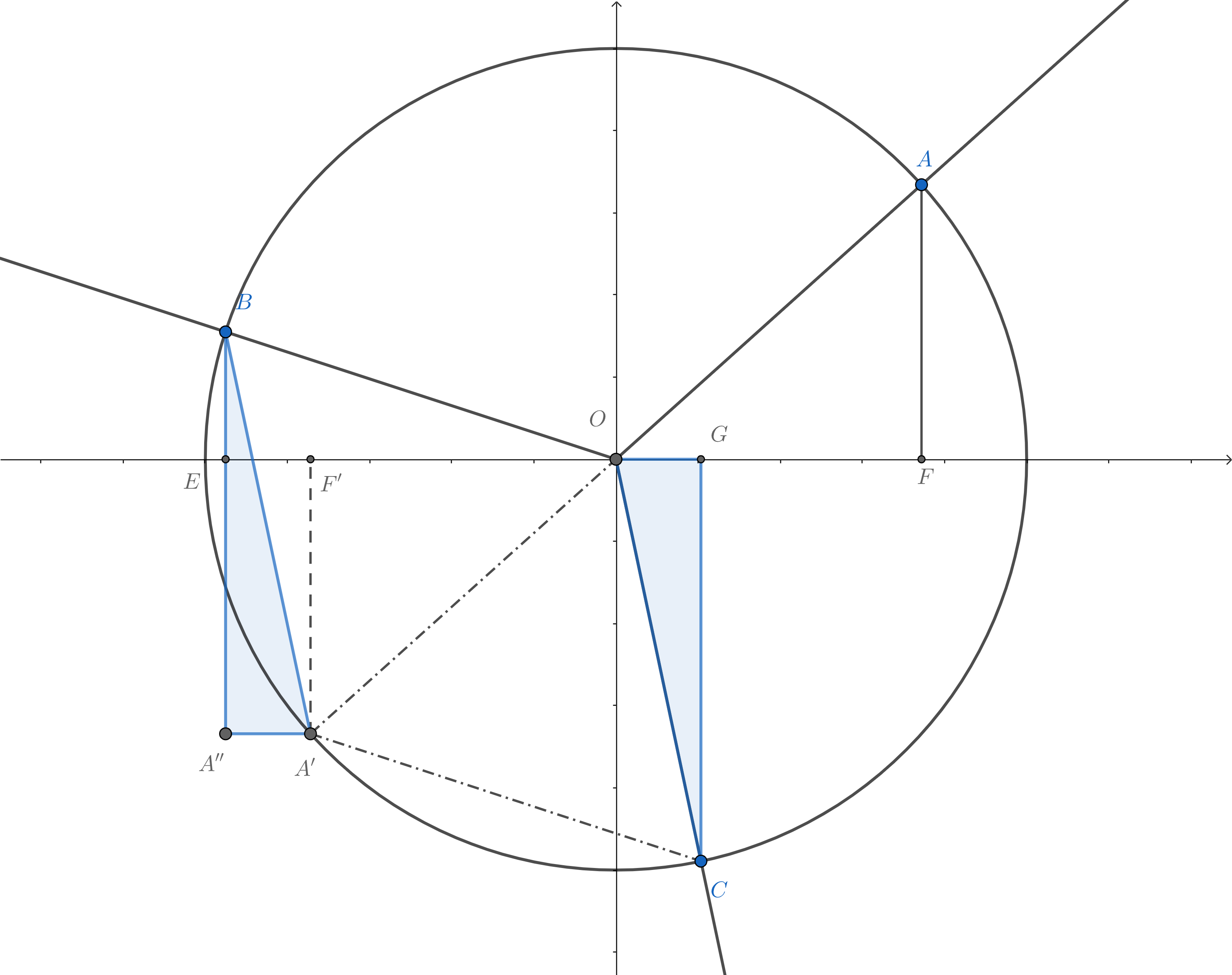如图，$A'$是$A$关于原点的对称点，$A'F'\perp x,A''B\parallel A'F',A''A'\parallel x$ 由$\triangle OBA'$和$\triangle OCA'$是等边三角形，易得$\triangle BA''A'\cong\triangle CGO$ 从而$CG=BA''=BE+AF$, 即$\sin A+\sin B+\sin C=0$ 同理可证$\cos A+\cos B+\cos C=0\quad\square$

三角恒等变换推导

由$\sin A+\sin B=-\sin C,\cos A+\cos B=-\cos C$，
得：
$$
\begin{aligned}
(\sin A+\sin B)^2+(\cos A+\cos B)^2&=\sin^2C+\cos^2C=1\\
2\sin A\sin B+2\cos A\cos B&=-1\\
\cos(A-B)&=-\frac{1}{2}
\end{aligned}
$$
即$A-B=\frac{2}{3}\pi+2k\pi$或$A-B=-\frac{2}{3}\pi+2k\pi$ ($k\in\mathbb{Z}$)
同理可证$B-C=\frac{2}{3}\pi+2k\pi$或$B-C=-\frac{2}{3}\pi+2k\pi$ ($k\in\mathbb{Z}$),
$A-C=\frac{2}{3}\pi+2k\pi$或$A-C=-\frac{2}{3}\pi+2k\pi$ ($k\in\mathbb{Z}$).
设$B>A>C$, 又由$A\not=B\not=C$, 易得$B=A+\frac{2}{3}\pi+2m\pi,A=C+\frac{2}{3}\pi+2n\pi,m,n\in\mathbb{Z}$, 即$A,B,C$的终边三等分圆.$\quad\square$

5. 原题的解决

$$\sin A+\sin B=-\sin C\quad\to\quad ①2\sin\frac{A+B}{2}\cos\frac{A-B}{2}=-\sin C$$
$$\cos A+\cos B=-\cos C\quad\to\quad ②2\cos\frac{A+B}{2}\cos\frac{A-B}{2}=-\cos C$$
∵若$\cos\frac{A-B}{2}=0$, 则$\cos C=\sin C=0$, 与$\cos^2C+\sin^2C=1$矛盾
∴$\cos\frac{A-B}{2}\not=0$

  1. 若$\cos\frac{A+B}{2}=\cos C=0$:
    则$C=-\frac{1}{2}\pi+2k\pi,A=\frac{1}{6}\pi+2m\pi,B=\frac{5}{6}\pi+2n\pi,k,n,m\in\mathbb{Z}$
    或$C=\frac{1}{2}\pi+2k\pi,A=\frac{7}{6}\pi+2m\pi,B=\frac{11}{6}\pi+2n\pi,k,n,m\in\mathbb{Z}$
    显然$\cos^2A+\cos^2B+\cos^2C=\frac{3}{2}$
    (原答案没有对此情况进行讨论)
  2. 若$\cos\frac{A+B}{2}\not=0$
    $①\div ②$得$\tan\frac{A+B}{2}=\tan C$
    $$\cos(A+B)=\frac{1-\tan^2\frac{A+B}{2}}{1+\tan^2\frac{A+B}{2}}=\frac{1-\tan^2C}{1+\tan^2C}=\cos2C$$$$
    \begin{aligned}
    \cos^2A+\cos^2B+\cos^2C&=\frac{1}{2}(1+\cos2A+1+\cos2B+1+\cos2C)\\
    &=\frac{3}{2}+\frac{1}{2}[2\cos(A+B)\cos(A-B)+\cos2C]\\
    &=\frac{3}{2}+\frac{1}{2}[2\cos2C\cdot(-\frac{1}{2}+\cos2C)]\\
    &=\frac{3}{2}+0\\
    &=\frac{3}{2}
    \end{aligned}
    $$

6. 一些结论

$$\cos\alpha+\cos(\alpha+\frac{2}{3}\pi)+\cos(\alpha+\frac{4}{3}\pi)=0$$
$$\sin\alpha+\sin(\alpha+\frac{2}{3}\pi)+\sin(\alpha+\frac{4}{3}\pi)=0$$
$$\cos^2\alpha+\cos^2(\alpha+\frac{2}{3}\pi)+\cos^2(\alpha+\frac{4}{3}\pi)=\frac{3}{2}$$
$$\sin^2\alpha+\sin^2(\alpha+\frac{2}{3}\pi)+\sin^2(\alpha+\frac{4}{3}\pi)=\frac{3}{2}$$

7. 推广

设$\alpha_1,\alpha_2,\alpha_3,\cdots\alpha_n(n\in\mathbb{Z},n\ge3)$是终边将单位圆n等分的一组角，则:
$$\cos\alpha_1+\cos\alpha_2+\cdots+\cos\alpha_n=0$$
$$\sin\alpha_1+\sin\alpha_2+\cdots+\sin\alpha_n=0$$
$$\cos^2\alpha_1+\cos^2\alpha_2+\cdots+\cos^2\alpha_n=\frac{n}{2}$$
$$\sin^2\alpha_1+\sin^2\alpha_2+\cdots+\sin^2\alpha_n=\frac{n}{2}$$
即:
$$\sum_{k=1}^{n}\cos(\alpha+\frac{k-1}{n}\cdot2\pi)=0$$
$$\sum_{k=1}^{n}\sin(\alpha+\frac{k-1}{n}\cdot2\pi)=0$$
$$\sum_{k=1}^{n}\cos^2(\alpha+\frac{k-1}{n}\cdot2\pi)=\frac{n}{2}$$
$$\sum_{k=1}^{n}\sin^2(\alpha+\frac{k-1}{n}\cdot2\pi)=\frac{n}{2}$$
还没有找到证明方法(三角函数水平太差了)，就以后再说吧。

……本来已经把这个忘了，直到看到这个：
数学装逼神器——高端三角恒等变换 https://zhuanlan.zhihu.com/p/161360664
突然想起还留了这么一个问题，然后感觉半年之后，我应该可以了。

对于第一个式子$\sum_{k=1}^{n}\cos(\alpha+\frac{k-1}{n}\cdot2\pi)=0$，先化简一下：
$$
\begin{aligned}
&\sum_{k=1}^{n}\cos(\alpha+\frac{k-1}{n}\cdot2\pi)\\
=&\sum_{k=1}^{n}\cos\alpha\cos(\frac{k-1}{n}\cdot2\pi)-\sum_{k=1}^{n}\sin\alpha\sin(\frac{k-1}{n}\cdot2\pi)\\
=&\cos\alpha\sum_{k=1}^{n}\cos(\frac{k-1}{n}\cdot2\pi)-\sin\alpha\sum_{k=1}^{n}\sin(\frac{k-1}{n}\cdot2\pi)
\end{aligned}
$$
这里的关键在于三角函数的基本等差求和公式：
$$
\begin{aligned}
&\sum_{k=1}^{n}\cos(\frac{k-1}{n}\cdot2\pi)\\
=&1+\cos\frac{2}{n}\pi+\cos\frac{4}{n}\pi+\cdots+\cos\frac{2n-2}{n}\pi\\
=&1+\frac{\cos\frac{2}{n}\pi\sin\frac{1}{n}\pi+\cos\frac{4}{n}\pi\sin\frac{1}{n}\pi+\cdots+\cos\frac{2n-2}{n}\pi\sin\frac{1}{n}\pi}{\sin\frac{1}{n}\pi}
\end{aligned}
$$
对分子积化和差，然后就能全部消掉，得到$\frac{1}{2}\sin\frac{2n-1}{n}\pi-\frac{1}{2}\sin\frac{1}{n}\pi=-\sin\frac{1}{n}\pi$，于是得到：
$$\sum_{k=1}^{n}\cos(\frac{k-1}{n}\cdot2\pi)=0$$
类似地：
$$\sum_{k=1}^{n}\sin(\frac{k-1}{n}\cdot2\pi)=0$$
于是原式得证，正弦的情况也差不多。

什么，居然还有这种操作？！好吧其实课上讲过，但一直没想到用，现在才想起来……

那么来看$\sum_{k=1}^{n}\cos^2(\alpha+\frac{k-1}{n}\cdot2\pi)=\frac{n}{2}$这个式子，降幂化简：
$$\sum_{k=1}^{n}\cos^2(\alpha+\frac{k-1}{n}\cdot2\pi)=\frac{n}{2}-\sum_{k=1}^{n}\cos(2\alpha+\frac{k-1}{n}\cdot4\pi)$$
接下来跟前面一样，得到：
$$\sum_{k=1}^{n}\cos(2\alpha+\frac{k-1}{n}\cdot4\pi)=0$$
于是原式得证。

Updated 2023, 7, 13