記一道三角函數題

Veröffentlicht am in
記一道離譜的題目，以及推出的一些結論

1. 題目

設三個角$A\not=B\not=C$，滿足:
$$\cos A+\cos B+\cos C=0,\quad\sin A+\sin B+\sin C=0$$
求證$\cos^2A+\cos^2B+\cos^2C=\frac{3}{2}$.

2. 簡化情況

令$C=-\frac{1}{2}\pi$, 則$\cos A+\cos B=0$,
又由$\sin C=-1,\sin A+\sin B+\sin C=0$得$\sin A=\sin B=\frac{1}{2}$, 即$A=\frac{1}{6}\pi,B=\frac{5}{6}\pi$.
易得$\cos^2A+\cos^2B+\cos^2C=\frac{3}{2}$.

3. 猜想

滿足條件的一組$A,B,C$的終邊三等分單位圓.

4. 證明

充分性的幾何證明

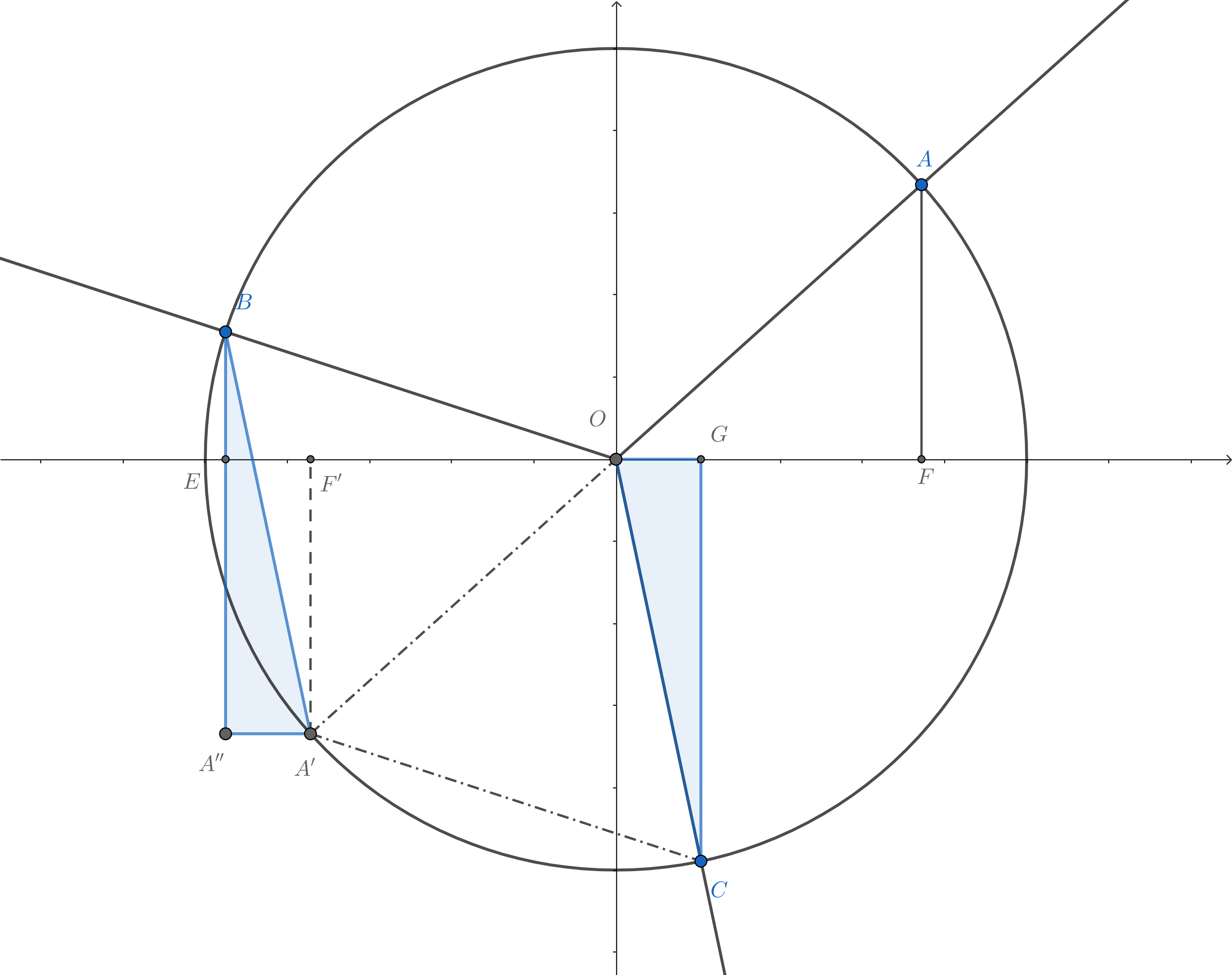如圖，$A'$是$A$關於原點的對稱點，$A'F'\perp x,A''B\parallel A'F',A''A'\parallel x$ 由$\triangle OBA'$和$\triangle OCA'$是等邊三角形，易得$\triangle BA''A'\cong\triangle CGO$ 從而$CG=BA''=BE+AF$, 即$\sin A+\sin B+\sin C=0$ 同理可證$\cos A+\cos B+\cos C=0\quad\square$

三角恆等變換推導

由$\sin A+\sin B=-\sin C,\cos A+\cos B=-\cos C$，
得：
$$
\begin{aligned}
(\sin A+\sin B)^2+(\cos A+\cos B)^2&=\sin^2C+\cos^2C=1\\
2\sin A\sin B+2\cos A\cos B&=-1\\
\cos(A-B)&=-\frac{1}{2}
\end{aligned}
$$
即$A-B=\frac{2}{3}\pi+2k\pi$或$A-B=-\frac{2}{3}\pi+2k\pi$ ($k\in\mathbb{Z}$)
同理可證$B-C=\frac{2}{3}\pi+2k\pi$或$B-C=-\frac{2}{3}\pi+2k\pi$ ($k\in\mathbb{Z}$),
$A-C=\frac{2}{3}\pi+2k\pi$或$A-C=-\frac{2}{3}\pi+2k\pi$ ($k\in\mathbb{Z}$).
設$B>A>C$, 又由$A\not=B\not=C$, 易得$B=A+\frac{2}{3}\pi+2m\pi,A=C+\frac{2}{3}\pi+2n\pi,m,n\in\mathbb{Z}$, 即$A,B,C$的終邊三等分圓.$\quad\square$

5. 原題的解決

$$\sin A+\sin B=-\sin C\quad\to\quad ①2\sin\frac{A+B}{2}\cos\frac{A-B}{2}=-\sin C$$
$$\cos A+\cos B=-\cos C\quad\to\quad ②2\cos\frac{A+B}{2}\cos\frac{A-B}{2}=-\cos C$$
∵若$\cos\frac{A-B}{2}=0$, 則$\cos C=\sin C=0$, 與$\cos^2C+\sin^2C=1$矛盾
∴$\cos\frac{A-B}{2}\not=0$

  1. 若$\cos\frac{A+B}{2}=\cos C=0$:
    則$C=-\frac{1}{2}\pi+2k\pi,A=\frac{1}{6}\pi+2m\pi,B=\frac{5}{6}\pi+2n\pi,k,n,m\in\mathbb{Z}$
    或$C=\frac{1}{2}\pi+2k\pi,A=\frac{7}{6}\pi+2m\pi,B=\frac{11}{6}\pi+2n\pi,k,n,m\in\mathbb{Z}$
    顯然$\cos^2A+\cos^2B+\cos^2C=\frac{3}{2}$
    (原答案沒有對此情況進行討論)
  2. 若$\cos\frac{A+B}{2}\not=0$
    $①\div ②$得$\tan\frac{A+B}{2}=\tan C$
    $$\cos(A+B)=\frac{1-\tan^2\frac{A+B}{2}}{1+\tan^2\frac{A+B}{2}}=\frac{1-\tan^2C}{1+\tan^2C}=\cos2C$$$$
    \begin{aligned}
    \cos^2A+\cos^2B+\cos^2C&=\frac{1}{2}(1+\cos2A+1+\cos2B+1+\cos2C)\\
    &=\frac{3}{2}+\frac{1}{2}[2\cos(A+B)\cos(A-B)+\cos2C]\\
    &=\frac{3}{2}+\frac{1}{2}[2\cos2C\cdot(-\frac{1}{2}+\cos2C)]\\
    &=\frac{3}{2}+0\\
    &=\frac{3}{2}
    \end{aligned}
    $$

6. 一些結論

$$\cos\alpha+\cos(\alpha+\frac{2}{3}\pi)+\cos(\alpha+\frac{4}{3}\pi)=0$$
$$\sin\alpha+\sin(\alpha+\frac{2}{3}\pi)+\sin(\alpha+\frac{4}{3}\pi)=0$$
$$\cos^2\alpha+\cos^2(\alpha+\frac{2}{3}\pi)+\cos^2(\alpha+\frac{4}{3}\pi)=\frac{3}{2}$$
$$\sin^2\alpha+\sin^2(\alpha+\frac{2}{3}\pi)+\sin^2(\alpha+\frac{4}{3}\pi)=\frac{3}{2}$$

7. 推廣

設$\alpha_1,\alpha_2,\alpha_3,\cdots\alpha_n(n\in\mathbb{Z},n\ge3)$是終邊將單位圓n等分的一組角，則:
$$\cos\alpha_1+\cos\alpha_2+\cdots+\cos\alpha_n=0$$
$$\sin\alpha_1+\sin\alpha_2+\cdots+\sin\alpha_n=0$$
$$\cos^2\alpha_1+\cos^2\alpha_2+\cdots+\cos^2\alpha_n=\frac{n}{2}$$
$$\sin^2\alpha_1+\sin^2\alpha_2+\cdots+\sin^2\alpha_n=\frac{n}{2}$$
即:
$$\sum_{k=1}^{n}\cos(\alpha+\frac{k-1}{n}\cdot2\pi)=0$$
$$\sum_{k=1}^{n}\sin(\alpha+\frac{k-1}{n}\cdot2\pi)=0$$
$$\sum_{k=1}^{n}\cos^2(\alpha+\frac{k-1}{n}\cdot2\pi)=\frac{n}{2}$$
$$\sum_{k=1}^{n}\sin^2(\alpha+\frac{k-1}{n}\cdot2\pi)=\frac{n}{2}$$
還沒有找到證明方法(三角函數水平太差了)，就以後再說吧。

……本來已經把這個忘了，直到看到這個：
數學裝逼神器——高端三角恆等變換 https://zhuanlan.zhihu.com/p/161360664
突然想起還留了這麼一個問題，然後感覺半年之後，我應該可以了。

對於第一個式子$\sum_{k=1}^{n}\cos(\alpha+\frac{k-1}{n}\cdot2\pi)=0$，先化簡一下：
$$
\begin{aligned}
&\sum_{k=1}^{n}\cos(\alpha+\frac{k-1}{n}\cdot2\pi)\\
=&\sum_{k=1}^{n}\cos\alpha\cos(\frac{k-1}{n}\cdot2\pi)-\sum_{k=1}^{n}\sin\alpha\sin(\frac{k-1}{n}\cdot2\pi)\\
=&\cos\alpha\sum_{k=1}^{n}\cos(\frac{k-1}{n}\cdot2\pi)-\sin\alpha\sum_{k=1}^{n}\sin(\frac{k-1}{n}\cdot2\pi)
\end{aligned}
$$
這裡的關鍵在於三角函數的基本等差求和公式：
$$
\begin{aligned}
&\sum_{k=1}^{n}\cos(\frac{k-1}{n}\cdot2\pi)\\
=&1+\cos\frac{2}{n}\pi+\cos\frac{4}{n}\pi+\cdots+\cos\frac{2n-2}{n}\pi\\
=&1+\frac{\cos\frac{2}{n}\pi\sin\frac{1}{n}\pi+\cos\frac{4}{n}\pi\sin\frac{1}{n}\pi+\cdots+\cos\frac{2n-2}{n}\pi\sin\frac{1}{n}\pi}{\sin\frac{1}{n}\pi}
\end{aligned}
$$
對分子積化和差，然後就能全部消掉，得到$\frac{1}{2}\sin\frac{2n-1}{n}\pi-\frac{1}{2}\sin\frac{1}{n}\pi=-\sin\frac{1}{n}\pi$，於是得到：
$$\sum_{k=1}^{n}\cos(\frac{k-1}{n}\cdot2\pi)=0$$
類似地：
$$\sum_{k=1}^{n}\sin(\frac{k-1}{n}\cdot2\pi)=0$$
於是原式得證，正弦的情況也差不多。

什麼，居然還有這種操作？！好吧其實課上講過，但一直沒想到用，現在才想起來……

那麼來看$\sum_{k=1}^{n}\cos^2(\alpha+\frac{k-1}{n}\cdot2\pi)=\frac{n}{2}$這個式子，降冪化簡：
$$\sum_{k=1}^{n}\cos^2(\alpha+\frac{k-1}{n}\cdot2\pi)=\frac{n}{2}-\sum_{k=1}^{n}\cos(2\alpha+\frac{k-1}{n}\cdot4\pi)$$
接下來跟前面一樣，得到：
$$\sum_{k=1}^{n}\cos(2\alpha+\frac{k-1}{n}\cdot4\pi)=0$$
於是原式得證。

Updated 2023, 7, 13